题目内容
【题目】已知函数![]() (
(![]() ,且
,且![]() ,e为自然对数的底).
,e为自然对数的底).
(I)求函数![]() 的单调区间
的单调区间
(Ⅱ)若函数![]() 在
在![]() 有两个不同零点,求a的取值范围.
有两个不同零点,求a的取值范围.
【答案】(I)当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;当
;当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I)![]() ,分
,分![]() ,
,![]() 两种情况讨论解不等式即可;
两种情况讨论解不等式即可;
(Ⅱ)因为![]() 有两个正零点,由(I)知
有两个正零点,由(I)知![]() 且
且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.当
上单调递增.当![]() ,当
,当![]() ,
,![]() ,所以只需
,所以只需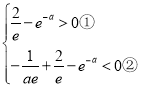 ,对于①直接解不等式,对于②,构造
,对于①直接解不等式,对于②,构造![]() ,结合单调性解决.
,结合单调性解决.
(I)由![]() ,知
,知![]()
①当![]() 时,定义域为
时,定义域为![]() 得
得![]() ,
,![]() 得
得![]() ;
;
②当![]() 时,定义域为
时,定义域为![]() 得
得![]() ,
,![]() 得
得![]()
所以,当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;
;
当![]() 时,增区间为
时,增区间为![]() ,减区间为
,减区间为![]() ;
;
(Ⅱ)因为![]() 有两个正零点,由(I)知
有两个正零点,由(I)知![]()
且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
设![]() 时,指数函数是爆炸增长,
时,指数函数是爆炸增长,![]() ,
,
当![]() ,当
,当![]() ,
,![]()
因为![]() 有两个正零点,所以有
有两个正零点,所以有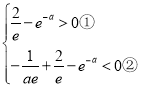 ,
,
由①得![]() ,
,
对于②,令![]() ,
,![]() ,
,
![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,由
,由![]() 知
知![]() ,
,
由②![]() 得
得![]()
综上所述,![]()
【点晴】
本题考查利用导数研究函数的单调性以及已知函数零点个数求参数范围的问题,考查学生逻辑推理能力,是一道中档题.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目