题目内容
【题目】已知椭圆E： 
=1的离心率为 
，点F1 ， F2是椭圆E的左、右焦点，过F1的直线与椭圆E交于A，B两点，且△F2AB的周长为8．
（1）求椭圆E的标准方程；
（2）动点M在椭圆E上，动点N在直线l：y=2 
上，若OM⊥ON，探究原点O到直线MN的距离是否为定值，并说明理由．
【答案】
（1）解：椭圆E： 
=1的离心率为 
，且△F2AB的周长为8，
所以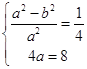 
，
解得a=2，b= 
，
所以椭圆E的标准方程为 
+ 
=1
（2）解：①若直线ON的斜率不存在，
则|OM|=2 ，|ON|=2，|MN|=4，
所以原点O到直线MN的距离为d= 
= ；
②若直线ON的斜率存在，
设直线OM方程为y=kx，
代入 + =1，解得x2= 
，
y2= 
；
则直线ON的方程为y=﹣ 
x，代入y=2 ，
解得N（﹣2 k，2 ）；
所以|MN|2=|OM|2+|ON|2=（ + ）+（12k2+12）= 
；
设原点O到直线MN的距离为d，
则|MN|d=|OM||ON|，
得d2=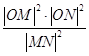 
=3，
所以d= ；
综上，原点O到直线MN的距离为定值
【解析】（1）根据题意列出方程组求出a、b的值，写出椭圆E的标准方程；（2）①直线ON的斜率不存在，计算原点O到直线MN的距离d的值；②直线ON的斜率存在，设出直线OM、ON的方程，求出点M、N，计算|MN|2、|OM|2、|ON|2，求出原点O到直线MN的距离d，即可得出结论．
练习册系列答案
相关题目
