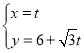Question

【题目】已知数列｛｝的前n项和为Sn，，且对任意的n∈N*，n≥2都有。

（1）若0，，求r的值；

（2）数列｛｝能否是等比数列？说明理由；

（3）当r＝1时，求证：数列｛｝是等差数列。

Answer 1

【答案】（1）1；（2）不可能是等比数列；（3）详见解析.

【解析】

（1）令，得到，再将和用项来表示，再结合条件，求得结果；

（2）假设其为等比数列，利用，结合，得到关于的方程，求解得出或，将其回代检验得出答案；

（3）将r＝1代入上式，类比着写出，两式相减得到，进一步凑成，结合，从而证得数列是以为首项，2为公差的等差数列.

（1）令n＝2，得：，

即：，

化简，得：，因为，，，

所以，，解得：r＝1.

（2）假设是等比数列，公比为，则，且，

解得或，

由，

可得，

所以，

两式相减，整理得，

两边同除以，可得，

因为，所以，

所以上式不可能对任意恒成立，故不可能是等比数列.

（3）时，令，整理得，

又由可知，

令，可得，解得，

由（2）可知，

所以，

两式相减，整理得，

所以，

两式相减，可得，

因为，所以，

即，又因为，

所以数列是以为首项，2为公差的等差数列.