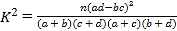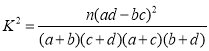题目内容
【题目】(1)若![]() ,是不等式
,是不等式![]() 成立的必要不充分条件,求实数的
成立的必要不充分条件,求实数的![]() 取值范围;
取值范围;
(2)已知集合![]() ,
,![]() .若“
.若“![]() ”是“
”是“![]() ”的充分条件,求实数
”的充分条件,求实数![]() 的取值范围;
的取值范围;
(3)已知命题“![]() ,
,![]() ”的否定为假命题,求实数
”的否定为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据题意,进而分离参数,由命题之间的关系,即可求得结果;
(2)根据“![]() ”是“
”是“![]() ”的充分条件,得到集合
”的充分条件,得到集合![]() 之间的包含关系,再根据集合之间的关系求参数范围即可;
之间的包含关系,再根据集合之间的关系求参数范围即可;
(3)根据命题的真假,由恒成立问题分离参数,求参数的范围即可.
(1)若![]() ,即
,即![]() ,
,
设![]() ,容易知其为单调增函数;
,容易知其为单调增函数;
根据题意不等式![]() 成立,则一定有
成立,则一定有![]() ,
,
也即![]() 一定可得到
一定可得到![]() .
.
因为![]() ,
,
故![]() 满足题意.
满足题意.
(2)因为![]()
求函数![]() 的值域,即可得
的值域,即可得![]()
又![]()
因为“![]() ”是“
”是“![]() ”的充分条件,
”的充分条件,
故可得集合![]() 是集合
是集合![]() 的真子集,
的真子集,
故只需满足:![]() ,
,
解得![]() .
.
(3)因为命题“![]() ,
,![]() ”的否定为假命题
”的否定为假命题
故![]() ,
,![]() 恒成立,
恒成立,
即可得![]() 恒成立.
恒成立.
又![]() ,
,
故只需![]() 即可,
即可,
解得![]() .
.

【题目】影响消费水平的原因很多,其中重要的一项是工资收入.研究这两个变量的关系的一个方法是通过随机抽样的方法,在一定范围内收集被调查者的工资收入和他们的消费状况.下面的数据是某机构收集的某一年内上海、江苏、浙江、安徽、福建五个地区的职工平均工资与城镇居民消费水平(单位:万元).
地区 | 上海 | 江苏 | 浙江 | 安徽 | 福建 |
职工平均工资 | 9.8 | 6.9 | 6.4 | 6.2 | 5.6 |
城镇居民消费水平 | 6.6 | 4.6 | 4.4 | 3.9 | 3.8 |
(1)利用江苏、浙江、安徽三个地区的职工平均工资和他们的消费水平,求出线性回归方程![]() ,其中
,其中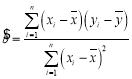
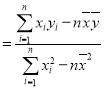 ,
,![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1万,则认为得到的线性回归方程是可靠的,试问所得的线性回归方程是否可靠?(![]() 的结果保留两位小数)
的结果保留两位小数)
(参考数据:![]() ,
,![]() )
)
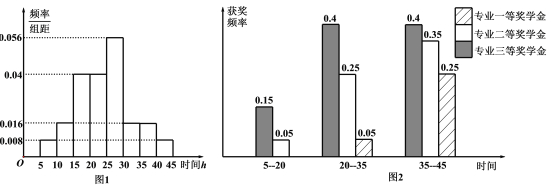
【题目】在中老年人群体中,肠胃病是一种高发性疾病某医学小组为了解肠胃病与运动之间的联系,调查了50位中老年人每周运动的总时长(单位:小时),将数据分成[0,4),[4,8),[8,14),[14,16),[16,20),[20,24]6组进行统计,并绘制出如图所示的柱形图.
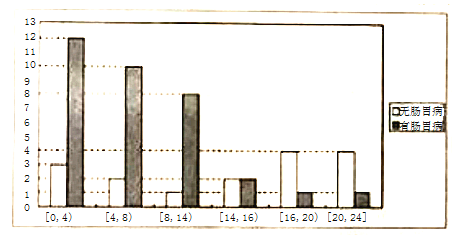
图中纵轴的数字表示对应区间的人数现规定:每周运动的总时长少于14小时为运动较少.
每周运动的总时长不少于14小时为运动较多.
(1)根据题意,完成下面的2×2列联表:
有肠胃病 | 无肠胃病 | 总计 | |
运动较多 | |||
运动较少 | |||
总计 |
(2)能否有99.9%的把握认为中老年人是否有肠胃病与运动有关?
附:K2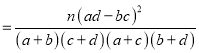 (n=a+b+c+d)
(n=a+b+c+d)
P(K2≥k) | 0.0.50 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |