题目内容
1.函数f(x)=sin2x+$\frac{\sqrt{2}}{2}$cos(2x+$\frac{π}{4}$)(1)求f(x)的最小正周期;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若b=$\sqrt{3}$且f($\frac{B}{2}$+$\frac{π}{4}$)=$\frac{1}{8}$,求△ABC的面积最大值.
分析 (1)由三角函数中的恒等变换应用化简解析式可得f(x)=$\frac{1}{2}-\frac{1}{2}$sin2x,由周期公式即可得解.
(2)利用诱导公式化简已知等式可得cosB=$\frac{3}{4}$,由余弦定理及基本不等式可得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}≥\frac{2ac-3}{2ac}$,解得ac≤6,由三角形面积公式即可得解.
解答 解:∵f(x)=sin2x+$\frac{\sqrt{2}}{2}$cos(2x+$\frac{π}{4}$)
=$\frac{\sqrt{2}}{2}$(cos2xcos$\frac{π}{4}$-sin2xsin$\frac{π}{4}$)$+\frac{1-cos2x}{2}$
=$\frac{1}{2}-\frac{1}{2}$sin2x
①T=$\frac{2π}{2}=π$.…(5分)
②∵f($\frac{B}{2}$+$\frac{π}{4}$)=$\frac{1}{2}-\frac{1}{2}$sin(B+$\frac{π}{2}$)=$\frac{1}{2}-\frac{1}{2}$cosB=$\frac{1}{8}$,
∴cosB=$\frac{3}{4}$,
在△ABC中,cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}≥\frac{2ac-3}{2ac}$,得ac≤6,
∴当a=c=$\sqrt{6}$时,${S}_{△ABC}≤\frac{1}{2}acsinB=\frac{1}{2}×6×\frac{\sqrt{7}}{4}=\frac{3\sqrt{7}}{4}$.…(12分)
点评 本题主要考查了三角函数中的恒等变换应用,周期公式,诱导公式,三角形面积公式,余弦定理及基本不等式的应用,属于基本知识的考查.

| A. | {an}是公比为2的等比数列 | B. | {an}是公比为3的等比数列 | ||
| C. | {an}是公差为2的等差数列 | D. | {an}是公差为3的等差数列 |
| A. | x2+(y-1)2=1 | B. | x2+(y+1)2=1 | C. | (x-1)2+y2=1 | D. | (x+1)2+y2=1 |
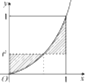 如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.
如图,由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是$\frac{1}{4}$.