题目内容
已知函数 图象的一部分如图所示.
图象的一部分如图所示.
(1)求函数 的解析式;
的解析式;
(2)当 时,求函数
时,求函数 的最大值与最小值及相应的
的最大值与最小值及相应的 的值.
的值.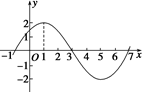
(1) ;(2)当x=-
;(2)当x=- 时,取得最大值
时,取得最大值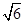 ,当x=-4时,取得最小值-2
,当x=-4时,取得最小值-2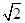 .
.
解析试题分析:(1)先根据图象得出最大值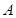 ,以及周期,从而求出
,以及周期,从而求出 的值,最后将最高点
的值,最后将最高点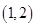 代入函数解析式并结合
代入函数解析式并结合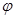 的取值范围得出
的取值范围得出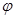 的值,从而确定函数
的值,从而确定函数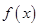 的解析式;(2)求出函数
的解析式;(2)求出函数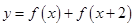 结合诱导公式以及辅助角公式将函数
结合诱导公式以及辅助角公式将函数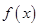 的解析式化简为
的解析式化简为 的形式,并计算出
的形式,并计算出 的取值范围,然后结合正弦曲线得到函数的最值,并找出相应的最值时,
的取值范围,然后结合正弦曲线得到函数的最值,并找出相应的最值时, 的值,从而求解出函数取最值时的
的值,从而求解出函数取最值时的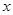 值.
值.
试题解析:(1)由图象知A=2,T=8,∵T=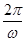 =8,∴ω=
=8,∴ω=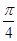 .又图象过点(-1,0),∴2sin
.又图象过点(-1,0),∴2sin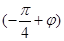 =0.∵|φ|<
=0.∵|φ|< ,∴φ=
,∴φ=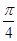 .∴
.∴ .(2)y=f(x)+f(x+2)=
.(2)y=f(x)+f(x+2)=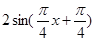 +
+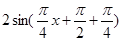 =
= =2
=2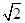 cos
cos 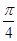 x.∵
x.∵ ,∴-
,∴- ≤
≤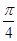 x≤-
x≤- .∴当
.∴当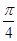 x=-
x=- ,即x=-
,即x=- 时,y=f(x)+f(x+2)取得最大值
时,y=f(x)+f(x+2)取得最大值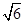 ;当
;当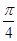 x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2
x=-π,即x=-4时,y=f(x)+f(x+2)取得最小值-2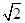 .
.
考点:1、三角函数图象与三角函数解析式;2、三角函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. 的值;
的值; 的值.
的值.
 的最小正周期;
的最小正周期; 时,若
时,若 ,求
,求 的值.
的值.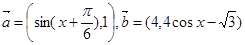
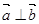 ,求
,求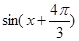 的值;
的值;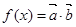 ,若
,若 ,求
,求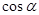 的值.
的值.  .
. 的单调递增区间;
的单调递增区间; 是
是 的三个内角,且
的三个内角,且 ,
, ,又
,又 ,求
,求 边的长.
边的长. .
. 的最小正周期和最值;
的最小正周期和最值; , 求证:
, 求证: .
. ,
, ,且
,且 .
. 的值;
的值; ,
, ,求
,求 .
.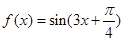 .
. 的单调递增区间;
的单调递增区间;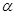 是第二象限角,
是第二象限角, ,求
,求 的值.
的值. (
( ,
, ,
, ),
), 的部分图像如图所示,
的部分图像如图所示, 、
、 分别为该图像的最高点和最低点,点
分别为该图像的最高点和最低点,点 .
. 的最小正周期及
的最小正周期及 的值;
的值; 的坐标为
的坐标为 ,
, ,求
,求 的值和
的值和 的面积.
的面积.