题目内容
【题目】在数列{an}中，a1＝1，a2＝2，数列{anan＋1}是公比为q (q>0)的等比数列，则数列{an}的前2n项和S2n＝____________.
【答案】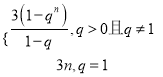
【解析】∵数列{anan＋1}是公比为q (q>0)的等比数列，
∴
，即
＝q，
这表明数列{an}的所有奇数项成等比数列，
所有偶数项成等比数列，且公比都是q，
又a1＝1，a2＝2，
∴当q≠1时，S2n＝a1＋a2＋a3＋a4＋…＋a2n－1＋a2n
＝(a1＋a3＋…＋a2n－1)＋(a2＋a4＋a6＋…＋a2n)
＝
；
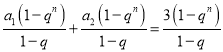当q＝1时，S2n＝a1＋a2＋a3＋a4＋…＋a2n－1＋a2n
＝(a1＋a3＋…＋a2n－1)＋(a2＋a4＋a6＋…＋a2n)
综上所述：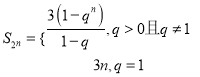 
.
练习册系列答案
寒假学与练系列答案
相关题目
