题目内容
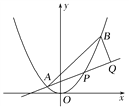
【题目】已知椭圆C: ![]() 的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为
的一个焦点与抛物线y2=-4x的焦点相同,且椭圆C上一点与椭圆C的左,右焦点F1,F2构成的三角形的周长为![]() .
.
(1)求椭圆C的方程;
(2)若直线l:y=kx+m(k,m∈R)与椭圆C交于A,B两点,O为坐标原点,△AOB的重心G满足: ![]() ,求实数m的取值范围.
,求实数m的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)利用与抛物线有公共焦点、椭圆的定义及几何要素间的等量关系进行求解;(2)联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用根与系数的关系、三角形的重心性质和平面向量的数量积运算进行求解.
的一元二次方程,利用根与系数的关系、三角形的重心性质和平面向量的数量积运算进行求解.
试题解析:(1)依题意得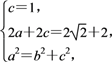
即![]()
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)设A(x1,y1),B(x2,y2),
联立得方程组![]()
消去y并整理得(1+2k2)x2+4kmx+2m2-2=0,
则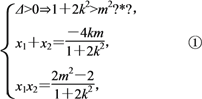
设△AOB的重心为G(x,y),
由![]() ·
·![]() =-
=-![]() ,
,
可得x2+y2=![]() .②
.②
由重心公式可得G(![]() ,
,![]() ),
),
代入②式,整理可得(x1+x2)2+(y1+y2)2=4(x1+x2)2+[k(x1+x2)+2m]2=4,③
将①式代入③式并整理,
得m2=![]() ,
,
代入(*)得k≠0,
则m2=![]() =1+
=1+![]() =1+
=1+![]() .
.
∵k≠0,∴t=![]() >0,∴t2+4t>0,
>0,∴t2+4t>0,
∴m2>1,∴m∈(-∞,-1)∪(1,+∞).

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目