题目内容
【题目】“双十一”期间，某淘宝店主对其商品的上架时间
（分钟）和销售量
（件）的关系作了统计，得到如下数据：
经计算： 
， 
， 
， 
.
（1）从满足
的数据
中任取两个，求所得两个数据都满足
的概率；
（2）该店主通过作散点图，发现上架时间与销售量线性相关，请你帮助店主求出上架时间与销售量的线性回归方程（保留三位小数），并预测商品上架1000分钟时的销售量.
【答案】(1) 
(2) 
,预测商品上架1000分钟时销售量约为2157件
【解析】试题分析：(1)由
得到满足题意的6个数据，从而明确了从中任取两个的所有结果为15，进而可得到所求的概率；（2）利用公式计算
， 
，得到回归直线方程，即可预测商品上架1000分钟时的销售量.
试题解析：
（1）由表知满足
的数据个数有6个，分别为127,133,136,138,142,147.
从中任取两个的所有结果为：
;
;
;
;
，
共15种.其中两个数据都满足
的结果有6种，故所求概率
（2）由题知： 
=
=
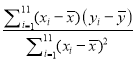=2.008
∴
=
=400-2.008125=149，∴回归直线方程为
；
当
时， 
，
故预测商品上架1000分钟时销售量约为2157件.
【题目】通过随机询问110名大学生是否爱好某项运动，得到列联表：
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由K2＝
，得K2＝
≈7.8.
附表：
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是( )
A. 有99%以上的把握认为“爱好该项运动与性别有关”
B. 有99%以上的把握认为“爱好该项运动与性别无关”
C. 在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”
D. 在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”
