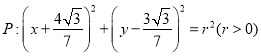题目内容
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,焦距为
,焦距为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,线段
,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴交于点
轴交于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1) ![]() (2)
(2) ![]() 或
或![]() .
.
【解析】试题分析:(1)根据题意可知![]() ,将点
,将点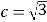 带入椭圆方程后联立方程组即可求得
带入椭圆方程后联立方程组即可求得![]() ,即可得到椭圆得标准方程;(2) 设
,即可得到椭圆得标准方程;(2) 设![]() ,线段
,线段![]() 中点坐标
中点坐标![]() ,由
,由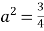 整理得:
整理得: ![]() ,结合韦达定理,线段
,结合韦达定理,线段![]() 的中点
的中点![]() 坐标,由
坐标,由![]() 可得点
可得点![]() 坐标,再由线段
坐标,再由线段![]() 的垂直平分线交
的垂直平分线交![]() 轴交于点
轴交于点![]() 及
及![]() ,求得
,求得![]() ,从而求出
,从而求出![]() 的值.
的值.
试题解析:(1)由题意得![]() ,所以
,所以![]() ,
,
又点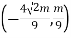 在椭圆上,
在椭圆上,
所以: 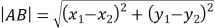 ,
,
整理得: ![]() ,
,
解得: ![]() 或
或![]() (舍),
(舍),
∴![]() ,
,
∴椭圆的标准方程为: ![]() .
.
(2)设![]() ,线段
,线段![]() 中点坐标
中点坐标![]() ,
,
由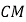 整理得:
整理得: ![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴线段![]() 的中点
的中点![]() 坐标为
坐标为
又![]()
![]() ,
,
∴![]() ,
,
又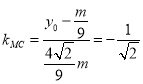 ,
,
∴![]() ,
,
∴点![]() 坐标为
坐标为![]() ,
,
∴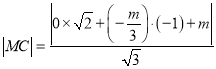
![]() ,
,
∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
又![]() ,
,
解得![]() 或
或![]() (舍),
(舍),
∴在![]() 中,
中, ![]()
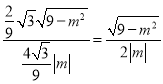 ,
,
∴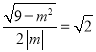 ,
,
∴![]() ,
,
∴![]() 或
或![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
【题目】设某地区乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
时间代号 | 1 | 2 | 3 | 4 | 5 | 6 |
储蓄存款 | 3.5 | 5 | 6 | 7 | 8 | 9.5 |
(1)求关于![]() 的回归方程
的回归方程![]() ,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
,并预测该地区2019年的人民币储蓄存款(用最简分数作答).
(2)在含有一个解释变量的线性模型中,![]() 恰好等于相关系数
恰好等于相关系数![]() 的平方,当
的平方,当![]() 时,认为线性回归模型是有效的,请计算
时,认为线性回归模型是有效的,请计算![]() 并且评价模型的拟合效果(计算结果精确到
并且评价模型的拟合效果(计算结果精确到![]() ).
).
附:
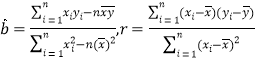 ,
, ![]() .
.