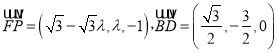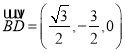题目内容
【题目】已知向量
= (1，2sinθ)，
= (sin(θ+
)，1)，θ
R。
(1) 若⊥，求 tanθ的值；
(2) 若∥，且 θ (0，
)，求 θ的值
【答案】（1）tanθ＝－
；（2）θ＝
.
【解析】
（1）利用两个向量垂直的坐标表示，列出方程，化简可求得
的值.（2）利用两个向量平行的坐标表示，列出方程，化简可求得
的值.
（1）依题意，得：
＝0，即
sin(θ+
)+2sinθ＝0，展开，得：
sinθcos＋cosθsin+2sinθ＝0，
化简，得：
sinθ＋
cosθ＝0，解得：tanθ＝－
（2）因为∥，所以，2sinθsin(θ+)＝1，展开得：
2sinθ（sinθcos＋cosθsin）＝1，
即：2sin2θ＋2
sinθcosθ＝2，
即：1－cos2θ＋sin2θ＝2，
化为：sin（2θ－）＝
，因为θ
(0，
)，所以，2θ－ (
)，
所以，2θ－＝，解得：θ＝
阅读快车系列答案
【题目】峰谷电是目前在城市居民当中开展的一种电价类别．它是将一天24小时划分成两个时间段，把8：00—22：00共14小时称为峰段，执行峰电价，即电价上调；22：00—次日8：00共10个小时称为谷段，执行谷电价，即电价下调．为了进一步了解民众对峰谷电价的使用情况，从某市一小区随机抽取了50 户住户进行夏季用电情况调查，各户月平均用电量以
，
，
，
，
，
（单位：度）分组的频率分布直方图如下图：
若将小区月平均用电量不低于700度的住户称为“大用户”，月平均用电量低于700度的住户称为“一般用户”．其中，使用峰谷电价的户数如下表：
月平均用电量（度） |
|
|
|
|
|
|
使用峰谷电价的户数 | 3 | 9 | 13 | 7 | 2 | 1 |
(1)估计所抽取的 50户的月均用电量的众数和平均数（同一组中的数据用该组区间的中点值作代表）；
(2)（
）将“一般用户”和“大用户”的户数填入下面
的列联表:
一般用户 | 大用户 | |
使用峰谷电价的用户 | ||
不使用峰谷电价的用户 |
(
)根据（）中的列联表，能否有
的把握认为 “用电量的高低”与“使用峰谷电价”有关？
| 0.025 | 0.010 | 0.001 |
| 5.024 | 6.635 | 10.828 |
附：
，
【题目】某电视台为宣传本市，随机对本市内
岁的人群抽取了
人，回答问题“本市内著名旅游景点有哪些” ，统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |
（1）分别求出
的值；
（2）根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数；
（3）若第1组回答正确的人员中，有2名女性，其余为男性，现从中随机抽取2人，求至少抽中1名女性的概率.
