题目内容
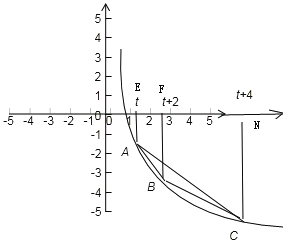
【题目】如图,A,B,C为函数![]() 的图象上的三点,它们的横坐标分别是t、t+2、t+4,其中t≥1,
的图象上的三点,它们的横坐标分别是t、t+2、t+4,其中t≥1,
.

(1)设△ABC的面积为S,求S=f(t);
(2)判断函数S=f(t)的单调性;
(3)求S=f(t)的最大值.
【答案】(1) S=![]()
(2) S=f(t)在![]() 是是减函数
是是减函数
(3) 最大值是f (1)=![]()
【解析】
解:(1)A、B、C三点坐标分别为(t,![]() t),(t+2,
t),(t+2,![]() (t+2)),(t+4,
(t+2)),(t+4,![]() (t+4)),由图形,当妨令三点A,B,C在x轴上的垂足为E,F,N,则△ABC的面积为
(t+4)),由图形,当妨令三点A,B,C在x轴上的垂足为E,F,N,则△ABC的面积为
SABC=S梯形ABFE+S梯形BCNF﹣S梯形ACNE
=﹣[![]() t
t![]() (t+2)]﹣[
(t+2)]﹣[![]() (t+2)
(t+2)![]() (t+4))]+2[
(t+4))]+2[![]() t
t![]() (t+4))]
(t+4))]
=[![]() t
t![]() (t+4)
(t+4)![]() (t+2)]
(t+2)]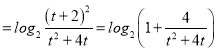
即△ABC的面积为S=f(t)![]() (t≥1)
(t≥1)
(2)f(t)![]() (t≥1)是复合函数,其外层是一个递增的函数,t≥1时,内层是一个递减的函数,故复合函数是一个减函数,
(t≥1)是复合函数,其外层是一个递增的函数,t≥1时,内层是一个递减的函数,故复合函数是一个减函数,
(3)由(2)的结论知,函数在t=1时取到最大值,故三角形面积的最大值是
S=f(1)![]()

练习册系列答案
相关题目
