题目内容
已知P、Q是椭圆C: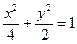 上的两个动点,
上的两个动点,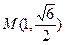 是椭圆上一定点,
是椭圆上一定点,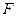 是其左焦点,且|PF|、|MF|、|QF|成等差数列。
是其左焦点,且|PF|、|MF|、|QF|成等差数列。
求证:线段PQ的垂直平分线经过一个定点A;
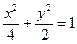 上的两个动点,
上的两个动点,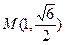 是椭圆上一定点,
是椭圆上一定点,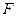 是其左焦点,且|PF|、|MF|、|QF|成等差数列。
是其左焦点,且|PF|、|MF|、|QF|成等差数列。求证:线段PQ的垂直平分线经过一个定点A;
证明略
【解题思路】利用“|PF|、|MF|、|QF|成等差数列”找出两动点间的坐标关系
证明:设
 知
知
同理
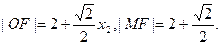

①当
 ,
,从而有

设线段PQ的中点为
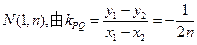 ,
, 得线段PQ的中垂线方程为
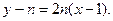

②当

线段PQ的中垂线是x轴,也过点

【名师指引】定点与定值问题的处理一般有两种方法:
(1)从特殊入手,求出定点和定值,再证明这个点(值)与变量无关;
(2)直接推理、计算,并在计算过程中消去变量,从而得到定点(定值).

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,讨论方程表示的曲线的形状
,讨论方程表示的曲线的形状 与曲线C恒有公共点,求
与曲线C恒有公共点,求 的取值范围.
的取值范围.
 ,-
,-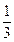 )
)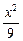 +
+ 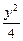 =1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是?
=1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是?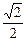 ,1)
,1)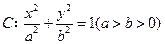 的左、右焦点分别是
的左、右焦点分别是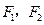 ,离心率为
,离心率为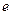 .直线
.直线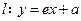 与
与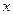 轴,
轴,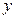 轴分别交于点
轴分别交于点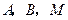 是直线
是直线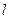 与椭圆
与椭圆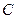 的一个公共点,
的一个公共点,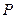 是点
是点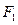 关于直线
关于直线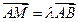 .
.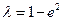 ;
;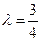 ,
,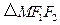 的周长为
的周长为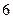 ,写出椭圆
,写出椭圆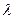 的值,使得
的值,使得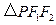 是等腰三角形.
是等腰三角形. ,
, ,
,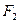 分别为其左、右焦点,
分别为其左、右焦点,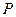 为椭圆上任意一点,
为椭圆上任意一点,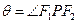 ,求
,求 的最大值及
的最大值及