题目内容
20.若实数x,y满足$\left\{\begin{array}{l}{2x-y+2≤0}\\{x+2y-4≥0}\\{x-3y+11≥0}\end{array}\right.$,则x,y所表示的区域的面积为$\frac{5}{2}$,若x,y同时满足(t+1)x+(t+2)y+t=0,则实数t的取值范围为[-2,-$\frac{4}{3}$].分析 作出不等式组对应的平面区域,求出三角形的交点坐标进行求解,求出(t+1)x+(t+2)y+t=0过定点,结合图象建立条件关系即可得到结论.
解答 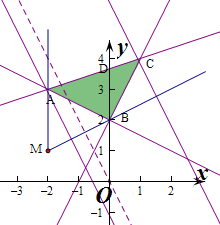 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).
由$\left\{\begin{array}{l}{2x-y+2=0}\\{x-3y+11=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$,即C(1,4),
由$\left\{\begin{array}{l}{x+2y-4=0}\\{x-3y+11=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=3}\end{array}\right.$,即A(-2,3),
由$\left\{\begin{array}{l}{2x-y+2=0}\\{x+2y-4=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$,即B(0,2),
令x=0.得y=$\frac{11}{3}$,即D(0,$\frac{11}{3}$),
即AD=$\frac{11}{3}$-2=$\frac{5}{3}$
则区域面积S=$\frac{1}{2}×$$\frac{5}{3}$×2+$\frac{1}{2}×$$\frac{5}{3}$×1=$\frac{5}{2}$.
由(t+1)x+(t+2)y+t=0得t(x+y+1)+x+2y=0,
由$\left\{\begin{array}{l}{x+y+1=0}\\{x+2y=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-2}\\{y=1}\end{array}\right.$,即(t+1)x+(t+2)y+t=0过定点M(-2,1),
则由图象知A,B两点在直线两侧和在直线上即可,
即[2(t+2)+t][-2(t+1)+3(t+2)+t]≤0,
即(3t+4)(2t+4)≤0,
解得-2≤t≤-$\frac{4}{3}$,
即实数t的取值范围为是[-2,-$\frac{4}{3}$],
故答案为:$\frac{5}{2}$;[-2,-$\frac{4}{3}$].
点评 本题主要考查线性规划的应用以及三角形面积的计算,利用数形结合是解决本题的关键.综合性较强,有一定的难度.

| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | log2$\frac{3}{2}$ | B. | log23 | C. | 1 | D. | 不存在 |
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
| A. | a>b>c>d | B. | a<b<c<d | C. | a>b>d>c | D. | b>a>c>d |