题目内容
7.已知二次函数f(x)=x2+bx+c,其中常数b,c∈R.(Ⅰ)若任意的x∈[-1,1],f(x)≥0,f(2+x)≤0,试求实数c的取值范围;
(Ⅱ)若对任意的x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,试求实数b的取值范围.
分析 (Ⅰ)若任意的x∈[-1,1],f(x)≥0,f(2+x)≤0,可得是f(1)=0,即1为函数函数f(x)的一个零点.由韦达定理,可得函数f(x)的另一个零点,进而可得实数c的取值范围;
(Ⅱ)若对任意的x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,f(x)max-f(x)min≤4,结合二次函数的图象和性质分类讨论,可得实数b的取值范围.
解答 解:(Ⅰ)因为x∈[-1,1],则2+x∈[1,3],
由已知,有对任意的x∈[-1,1],f(x)≥0恒成立,
任意的x∈[1,3],f(x)≤0恒成立,
故f(1)=0,即1为函数函数f(x)的一个零点.
由韦达定理,可得函数f(x)的另一个零点,
又由任意的x∈[1,3],f(x)≤0恒成立,
∴[1,3]⊆[1,c],
即c≥3
(Ⅱ)函数f(x)=x2+bx+c对任意的x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4恒成立,
即f(x)max-f(x)min≤4,
记f(x)max-f(x)min=M,则M≤4.
当|$-\frac{b}{2}$|>1,即|b|>2时,M=|f(1)-f(-1)|=|2b|>4,与M≤4矛盾;
当|$-\frac{b}{2}$|≤1,即|b|≤2时,M=max{f(1),f(-1)}-f($-\frac{b}{2}$)=$\frac{f(1)+f(-1)+|f(1)-f(-1)|}{2}$-f($-\frac{b}{2}$)=(1+$\frac{\left|b\right|}{2}$)2≤4,
解得:|b|≤2,
即-2≤b≤2,
综上,b的取值范围为-2≤b≤2.
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
17.若变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≤8}\\{2y-x≤4}\\{x≥0}\\{y≥0}\end{array}\right.$,且z=4y-x的最大值为a,最小值为b,则a+b的值是( )
| A. | 10 | B. | 20 | C. | 4 | D. | 12 |
15.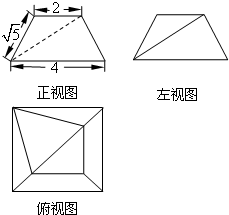 已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )
已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )
 已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )
已知一空间几何体的三视图如题图所示,其中正视图与左视图都是全等的等腰梯形,则该几何体的体积为( )| A. | 17 | B. | $\frac{52}{3}$ | C. | $\frac{55}{3}$ | D. | 18 |
12.设变量x、y满足线性约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$则目标函数z=log2(2x+y)的最大值为( )
| A. | log2$\frac{3}{2}$ | B. | log23 | C. | 1 | D. | 不存在 |
19.将甲,乙等5位同学分别保送到北京大学,复旦大学,中国科技大学就读,则每所大学至少保送一人的不同保送的方法数共有( )种.
| A. | 240 | B. | 180 | C. | 150 | D. | 540 |