Question

【题目】已知数列{an}满足条件an+1= ．
（1）若a1= ，求a2 ， a3 ， a4的值．
（2）已知对任意的n∈N+ ， 都有an≠1，求证：an+3=an对任意的正整数n都成立；
（3）在（1）的条件下，求a2015 ．

Answer 1

【答案】
（1）解：由数列{an}满足条件an+1= ，a1= ，

∴a2= =2，同理可得：a3=﹣1，a4=

（2）证明：∵ ，

∴ ，

∴ ．

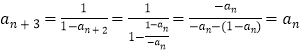即an+3=an对任意的正整数n都成立

（3）解：由前面的结论，可得a2015=a671×3+2=a2=2
【解析】（1）由数列{an}满足条件an+1= ，a1= ，分别令n=1，2，3，即可得出．（2）由于 ，利用递推公式可得：an+2= ，an+3=an ． （3）由前面的结论，可得a2015=a671×3+2=a2 ．
【考点精析】本题主要考查了数列的通项公式的相关知识点，需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．