Question

【题目】某人在塔的正东方向沿着南偏西60°的方向前进40 m以后，望见塔在东北方向上，若沿途测得塔的最大仰角为30°，则塔高为________________m．

Answer 1

【答案】

【解析】

根据题意作出示意图：

，

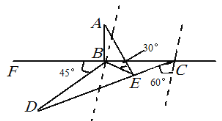此人在C处，AB为塔高，他沿CD前进，CD=40 m，此时∠DBF=45°，从点C到点D所测塔的仰角，只有点B到CD的距离最短时，仰角最大，这是因为为定值．根据正弦定理可解中的，在中求，再在中求塔高即可.

画示意图如下图所示，

此人在C处，AB为塔高，他沿CD前进，CD=40 m，此时∠DBF=45°，从点C到点D所测塔的仰角，只有点B到CD的距离最短时，仰角最大，这是因为为定值．

过点B作BE⊥CD于点E，连接AE，则 ．

在中，CD=40 m，∠BCD=30°，∠DBC=135°，

由正弦定理，得，∴

在中，

∴

在中，，∴

故所求的塔高为