题目内容
【题目】如图,在三棱锥P-ABC中,![]() ,
,![]() 底面ABC.
底面ABC.

(1)求证:平面![]() 平面PBC;
平面PBC;
(2)若![]() ,M是PB的中点,求AM与平面PBC所成角的正切值.
,M是PB的中点,求AM与平面PBC所成角的正切值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据题意,得到![]() 和
和![]() ,证得
,证得![]() 平面PAC,再由面面垂直的判定定理,即可得到平面
平面PAC,再由面面垂直的判定定理,即可得到平面![]() 平面PBC.
平面PBC.
(2)取PC的中点D,连接AD,DM,得出DM是斜线AM在平面PBC上的射影,得到![]() 是AM与平面PBC所成角,再由
是AM与平面PBC所成角,再由![]() ,即可求解.
,即可求解.
(1)由题意,因为![]() 面ABC,
面ABC,![]() 面ABC,
面ABC,![]() ,
,
又![]() ,即
,即![]() ,
,![]() ,
,![]() 平面PAC,
平面PAC,
![]() 平面PBC,∴平面
平面PBC,∴平面![]() 平面PBC.
平面PBC.
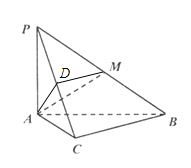
(2)取PC的中点D,连接AD,DM.![]() .
.
由(1)知,![]() 平面PAC,
平面PAC,
又![]() 平面PAC,
平面PAC,![]() .而
.而![]() .
.![]() 平面PBC,
平面PBC,
所以DM是斜线AM在平面PBC上的射影,
所以![]() 是AM与平面PBC所成角,且
是AM与平面PBC所成角,且![]() ,
,
设![]() ,则由M是PB中点得
,则由M是PB中点得![]() ,
,
![]() ,所以
,所以![]() ,
,
即AM与平面PBC所成角的正切值为![]() .
.

练习册系列答案
相关题目
【题目】十八大以来,我国新能源产业迅速发展.以下是近几年某新能源产品的年销售量数据:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
新能源产品年销售 | 1.6 | 6.2 | 17.7 | 33.1 | 55.6 |
(1)请画出上表中年份代码![]() 与年销量
与年销量![]() 的数据对应的散点图,并根据散点图判断.
的数据对应的散点图,并根据散点图判断.
![]() 与
与![]() 中哪一个更适宜作为年销售量
中哪一个更适宜作为年销售量![]() 关于年份代码
关于年份代码![]() 的回归方程类型;
的回归方程类型;
(2)根据(Ⅰ)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
的回归方程,并预测2019年某新能源产品的销售量(精确到0.01).
参考公式: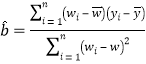 ,
,![]() .
.
参考数据: ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.