题目内容

【题目】如图，四棱锥P﹣ABCD的底面是边长为1的正方形，侧棱PA⊥底面ABCD，且PA=2，E是侧棱PA的中点．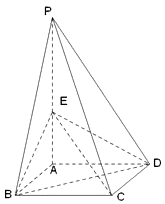
（1）求证：PC∥平面BDE
（2）求三棱锥P﹣CED的体积．

【答案】
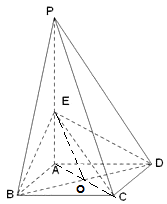
（1）证明：连结AC、BD，交于点O，连结OE，

∵四棱锥P﹣ABCD的底面是边长为1的正方形，

∴O是AC中点，

∵E是侧棱PA的中点，∴OE∥PC，

∵PC平面BDE，OE平面BDE，

∴PC∥平面BDE


（2）解：∵四棱锥P﹣ABCD的底面是边长为1的正方形，

侧棱PA⊥底面ABCD，且PA=2，E是侧棱PA的中点，

∴PA⊥CD，AD⊥CD，

∵PA∩AD=A，∴CD⊥平面PAD，

∵S△PDE= = = ，

∴三棱锥P﹣CED的体积VP﹣CED=VC﹣PDE= = = ．


【解析】（1）连结AC、BD，交于点O，连结OE，则OE∥PC，由此能证明PC∥平面BDE．（2）三棱锥P﹣CED的体积VP﹣CED=VC﹣PDE，由此能求出结果．

练习册系列答案
相关题目

【题目】一直线l过直线l1：3x﹣y=3和直线l2：x﹣2y=2的交点P，且与直线l3：x﹣y+1=0垂直．
（1）求直线l的方程；
（2）若直线l与圆心在x正半轴上的半径为 的圆C相切，求圆C的标准方程．

【题目】已知函数g（x）=ax2﹣2ax+1+b（a≠0，b＜1），在区间[2，3]上有最大值4，最小值1，设f（x）= ．
（1）求a，b的值；
（2）不等式f（2x）﹣k2x≥0在x∈[﹣1，1]上恒成立，求实数k的取值范围；
（3）方程f（|2x﹣1|）+k（ ﹣3）有三个不同的实数解，求实数k的取值范围．

【题目】已知函数f（x）=x2+2bx+c，且f（1）=f（3）=﹣1．设a＞0，将函数f（x）的图象先向右平移a个单位长度，再向下平移a2个单位长度，得到函数g（x）的图象． （Ⅰ）若函数g（x）有两个零点x1 ， x2 ， 且x1＜4＜x2 ， 求实数a的取值范围；
（Ⅱ）设连续函数在区间[m，n]上的值域为[λ，μ]，若有 ，则称该函数为“陡峭函数”．若函数g（x）在区间[a，2a]上为“陡峭函数”，求实数a的取值范围．

【题目】已知定点F（1，0），动点P（异于原点）在y轴上运动，连接FP，过点P作PM交x轴于点M，并延长MP到点N，且 ， ．
（1）求动点N的轨迹C的方程；
（2）若直线l与动点N的轨迹交于A、B两点，若 且 ，求直线l的斜率k的取值范围．

【题目】已知抛物线C：y2=4x，过焦点F作与x轴垂直的直线l1 ， C上任意一点P（x0 ， y0）（y0≠0）处的切线为l，l与l1交于M，l与准线交于N，则 = ．

【题目】动点P，Q从点A（1，0）出发沿单位圆运动，点P按逆时针方向每秒钟转 弧度，点Q按顺时针方向每秒钟转 弧度，设P，Q第一次相遇时在点B，则B点的坐标为 ．

【题目】如图：四棱锥P﹣ABCD中，底面ABCD是平行四边形，且AC=BD，PA⊥底面ABCD，PA=AB=1， ，点F是PB的中点，点E在边BC上移动．
（1）证明：当点E在边BC上移动时，总有EF⊥AF；
（2）当CE等于何值时，PA与平面PDE所成角的大小为45°．

【题目】已知函数f（x）= ，若|f（x）|≥ax，则a的取值范围是（ ）
A.（﹣∞，0]
B.（﹣∞，1]
C.[﹣2，1]
D.[﹣2，0]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网