题目内容

7．已知F是抛物线C：y2=4x的焦点，过点F的直线交抛物线C与A、B两点，且|AB|=6，则弦AB中点的横坐标为（　　）
A．1B．2C．4D．无法确定

分析 先根据抛物线方程求出p的值，再由抛物线的性质可得到答案．

解答 解：∵抛物线y2=4x，∴P=2，
设经过点F的直线与抛物线相交于A、B两点，
其横坐标分别为x1，x2，利用抛物线定义，
AB中点横坐标为x0=$\frac{1}{2}$（x1+x2）=$\frac{1}{2}$（|AB|-P）=$\frac{1}{2}$（6-2）=2．
故选：B．

点评 本题主要考查了抛物线的性质．属中档题．解题时要认真审题，仔细解答，注意等价转化思想的合理运用．

练习册系列答案
相关题目
17．一台仪器每启动一次都随机地出现一个5位的二进制数$A=\overline{{a_1}{a_2}{a_3}{a_4}{a_5}}$，其中A的各位数字中a1=1，ak（k=2，3，4，5）出现0的概率为$\frac{1}{3}$，ak（k=2，3，4，5）出现1的概率为$\frac{2}{3}$，记X=a1+a2+a3+a4+a5．当启动仪器一次时，
（Ⅰ）求X=3的概率；
（Ⅱ）求随机变量X的分布列及X的数学期望，并指出当X为何值时，其概率最大．
18．定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$，函数$f（x）=|{\begin{array}{l}{2sinx}&m\\{cos2x}&{cosx}\end{array}}|$的图象关于直线x=$\frac{π}{8}$对称，则f（x）的单调递增区间为（　　）
A．$[kπ-\frac{3π}{8}，kπ+\frac{π}{8}]，（k∈Z）$B．$[kπ-\frac{π}{8}，kπ+\frac{3π}{8}]，（k∈Z）$
C．$[2kπ-\frac{3π}{4}，2kπ+\frac{π}{4}]，（k∈Z）$D．$[2kπ-\frac{π}{4}，2kπ+\frac{3π}{4}]，（k∈Z）$
15．已知f（x）=ax2+bx+c（a＞0），y=f（x）-x的零点为x1，x2，且0＜x1＜x2＜$\frac{1}{a}$．
（1）当x∈（0，x1），求证：x＜f（x）＜x1．
（2）若x=x0为y=f（x）的对称轴，求证：x0＜$\frac{{x}_{1}}{2}$．
2．在△ABC中，内角A，B，C所对的边分别为a，b，c．已知a≠b，c=$\sqrt{3}$，cos2A-cos2B=$\sqrt{3}$sinAcosA-$\sqrt{3}$sinBcosB
（1）求角C的大小；
（2）求△ABC的面积的最大值．
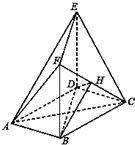12．如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点．
（1）求证：AC⊥平面BDEF；
（2）求二面角H-BD-C的大小．
19．若函数f（x）在定义域的某子区间上满足f（x）=$\frac{1}{λ}f（{x-λ}）$（λ为正实数），则称其为λ-局部倍缩函数．若函数f（x）在x∈[0，2]时，f（x）=sinπx，且x∈（2，+∞）时，f（x）为λ=2的局部倍缩函数．现有下列4个命题：
①任取x1、x2∈[0，+∞），都有|f（x1）-f（x2）|≤2恒成立；
②f（x）=2kf（x+2k）（k∈N*），对于一切x∈[0，+∞）恒成立；③函数y=f（x）-ln（x-1）有5个零点；④对任意x＞0，若不等式f（x）≤$\frac{k}{x}$恒成立，则k的最小值是$\frac{5}{4}$．
则其中所有真命题的序号是①④．
8．已知椭圆C：$\frac{x^2}{4}+{y^2}$=1，过原点的直线与椭圆C交于A，B两点（A，B不是椭圆C的顶点）．点D在椭圆C上，且AD⊥AB，直线BD与x轴、y轴分别交于M，N两点．
（1）设直线BD，AM的斜率分别为k1，k2，证明存在常数λ使得k1=λk2，并求出λ的值；
（2）求△OMN面积的最大值．
9．在直角坐标系中，已知点F（0，1），直线l：y=-1，点H是直线l上任意一点，过点H垂直于l的直线交线段FH的中垂线于点M．记点M的轨迹为曲线Γ．
（Ⅰ）求曲线Γ的方程；
（Ⅱ）若A，B为曲线Γ上异于原点的任意两点，过A，B分别作曲线T的两条切线l1、l2，l1、l2相交于点P，且与x轴分别交于E、F，设△PEF与△OAB的面积分别为S1、S2．试问：是否存在实数λ使得S1=λS2？若存在，求出λ的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网