题目内容
2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a≠b,c=$\sqrt{3}$,cos2A-cos2B=$\sqrt{3}$sinAcosA-$\sqrt{3}$sinBcosB(1)求角C的大小;
(2)求△ABC的面积的最大值.
分析 (1)利用二倍角公式、两角和差的正弦公式化简已知的式子,再由内角的范围求出角C;
(2)由余弦定理和条件列出方程化简,利用基本不等式求出ab的范围,代入三角形的面积公式可求出△ABC面积的最大值.
解答 解:(1)∵cos2A-cos2B=$\sqrt{3}$sinAcosA-$\sqrt{3}$sinBcosB,
∴$\frac{1+cos2A}{2}$-$\frac{1+cos2B}{2}$=$\frac{\sqrt{3}}{2}sin2A$$-\frac{\sqrt{3}}{2}sin2B$,
则cos2A-cos2B=$\sqrt{3}$(sin2A-sin2B),
即$\sqrt{3}$sin2B-cos2B=$\sqrt{3}$sin2A-cos2A,
∴sin($2B-\frac{π}{6}$)=sin($2A-\frac{π}{6}$)
∵a≠b,且A、B∈(0,π),
∴A≠B,则$2A-\frac{π}{6}$≠$2B-\frac{π}{6}$,
∴$2A-\frac{π}{6}+(2B-\frac{π}{6})=π$,解得A+B=$\frac{2π}{3}$,
∴C=π-A-B=$\frac{π}{3}$;
(2)由(1)知,C=$\frac{π}{3}$,且c=$\sqrt{3}$,
由余弦定理得,c2=a2+b2-2abcosC,
则3=a2+b2-ab,即a2+b2=ab+3≥2ab,
解得ab≤3,
∴△ABC的面积S=$\frac{1}{2}absinC$=$\frac{\sqrt{3}}{4}$ab≤$\frac{3\sqrt{3}}{4}$,
故△ABC的面积的最大值是$\frac{3\sqrt{3}}{4}$.
点评 本题考查了余弦定理,二倍角公式、两角和差的正弦公式,以及三角形的面积公式,基本不等式求最值问题,注意三角形内角的范围,属于中档题.

 英才计划期末调研系列答案
英才计划期末调研系列答案| A. | $\frac{2}{π}$ | B. | $\frac{1}{π}$ | C. | $\frac{π}{4}$ | D. | $\frac{1}{2π}$ |
| A. | 0 | B. | 80 | C. | -80 | D. | -32 |
| A. | 1 | B. | 2 | C. | 4 | D. | 无法确定 |
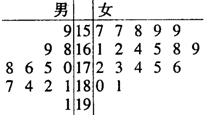 2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.
2013年8月28日-30日,第六届豫商大会在“三商之源、华商之都”的商丘市举行,为了搞好接待工作,大会组委会在某学院招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如所示的茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高个子”,身高在175cm以下(不包括175cm)定义为“非高个子”,且只有“女高个子”才担任“礼仪小姐”.