题目内容
一桥拱的形状为抛物线,已知该抛物线拱的宽为8米,抛物线拱的面积为160平方米,则抛物线拱的高等于
30
试题分析:设抛物线的高为h,那么根据定积分的几何意义可知抛物线拱的面积
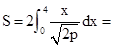 160,那么得到 p=
160,那么得到 p=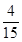 ,故可知抛物线拱的高30.故答案为30.
,故可知抛物线拱的高30.故答案为30.点评:解决该试题的关键是利用定积分表示出抛物线拱的面积,然后借助于定积分的给弄个是得到关于其结论。

练习册系列答案
相关题目
题目内容
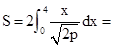 160,那么得到 p=
160,那么得到 p=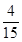 ,故可知抛物线拱的高30.故答案为30.
,故可知抛物线拱的高30.故答案为30.