题目内容
19.已知数列{an}的各项均不为0,其前n和为Sn,且满足a1=a,2Sn=anan+1.(Ⅰ)求a2的值;
(Ⅱ)求{an}的通项公式;
(Ⅲ)若a=-9,求Sn的最小值.
分析 (Ⅰ)由2Sn=anan+1,可得2a1=a1a2,又a1=a≠0,即可得出a2.
(Ⅱ)由2Sn=anan+1,可得an+1-an-1=2,于是数列{a2k-1},{a2k}都是公差为2的等差数列,即可得出.
(Ⅲ)当a=-9时,an=$\left\{\begin{array}{l}{n-10,n为奇数}\\{n,n为偶数}\end{array}\right.$,利用2Sn=anan+1,可得Sn,再利用二次函数的单调性即可得出.
解答 解:(Ⅰ)∵2Sn=anan+1,∴2S1=a1a2,即2a1=a1a2,
∵a1=a≠0,∴a2=2.
(Ⅱ)∵2Sn=anan+1,∴当n≥2时,2Sn-1=an-1an,
两式相减得到:2an=an(an+1-an-1),
∵an≠0,
∴an+1-an-1=2,
∴数列{a2k-1},{a2k}都是公差为2的等差数列,
当n=2k-1时,an=a1+2(k-1)=a+2k-2=a+n-1,
当n=2k时,an=2+2(k-1)=2k=n,
∴an=$\left\{\begin{array}{l}{n+a-1,n为奇数}\\{n,n为偶数}\end{array}\right.$.
(Ⅲ)当a=-9时,
an=$\left\{\begin{array}{l}{n-10,n为奇数}\\{n,n为偶数}\end{array}\right.$,
∵2Sn=anan+1,
∴Sn=$\left\{\begin{array}{l}{\frac{1}{2}(n-1)(n+1),n为奇数}\\{\frac{1}{2}n(n-9),n为偶数}\end{array}\right.$,
∴当n为奇数时,Sn的最小值为S5=-15;
当n为偶数时,Sn的最小值为S4=-10,
所以当n=5时,Sn取得最小值为-15.
点评 本题考查了递推关系的应用、等差数列的通项公式、分类讨论方法,考查了推理能力与计算能力,属于中档题.

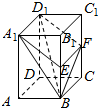 长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.
长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.