题目内容
9.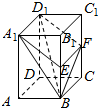 长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.
长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,求四棱锥B-A1EFD1的体积.
分析 作BM⊥A1E,交A1E延长线于M,由已知条件求出四棱锥B-A1EFD1的高BM=1×cos45°=$\frac{\sqrt{2}}{2}$,由此能求出四棱锥B-A1EFD1的体积.
解答  解:作BM⊥A1E,交A1E延长线于M,
解:作BM⊥A1E,交A1E延长线于M,
∵长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E、F分别为侧棱BB1、CC1的中点,
∴A1D1⊥平面ABB1A1,
∵BM?平面ABB1A1,
∴BM⊥A1D1,∵A1D1∩A1E=A,∴BM⊥平面A1EFD1,
∵A1B1=B1E=BE=1,∴∠BEM=∠A1EB1=45°,∠BMC=90°,
∴四棱锥B-A1EFD1的高BM=1×cos45°=$\frac{\sqrt{2}}{2}$,
${S}_{矩形{A}_{1}EF{D}_{1}}$=A1E×A1D1=$\sqrt{1+1}$×1=$\sqrt{2}$,
∴四棱锥B-A1EFD1的体积V=$\frac{1}{3}×{S}_{矩形{A}_{1}EF{D}_{1}}×BM$=$\frac{1}{3}×\sqrt{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{3}$.
点评 本题考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
20.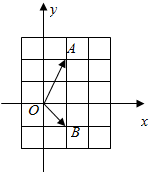 如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )
如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )
 如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )
如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.若三棱锥的三条侧棱两两垂直,且侧棱长都相等,其外接球的表面积是4π,则其侧棱长为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{\sqrt{2}}{3}$ |
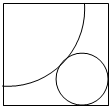 如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.
如图,在边长为5+$\sqrt{2}$的正方形纸片中剪下如图所示的扇形和圆,使它恰好成同一圆锥的侧面和底面,求此圆锥的体积.