题目内容
11.(1)计算:log2.56.25+lg$\frac{1}{100}$+ln$\sqrt{e}$+${2}^{1+lo{g}_{2}3}$;(2)已知x+x-1=3,求x2-x-2.
分析 (1)根据对数的运算性质即可求出;
(2)根据指数幂的运算性质即可求出.
解答 解:(1)原式=${log_{2.5}}{2.5^2}+lg{10^{-2}}+ln{e^{\frac{1}{2}}}+{2^{{{log}_2}6}}$=$2-2+\frac{1}{2}+6=\frac{13}{2}$,
(2)∵x+x-1=3,
∴(x-x-1)2=(x+x-1)2-4=9-4=5,
∴x-x-1=$±\sqrt{5}$,
∴x2-x-2=(x+x-1)(x-x-1)=$±3\sqrt{5}$
点评 本题考查了对数的运算性质和指数幂的运算性质,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且其图象向右平移$\frac{π}{6}$个单位后得到函数g(x)=sin(ωx)的图象,则函数f(x)的图象( )
| A. | 关于直线x=$\frac{π}{12}$对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{π}{12}$,0)对称 | D. | 关于点($\frac{5π}{12}$,0)对称 |
16.下列函数中,在R上是偶函数,且在(0,+∞)上为单调递增函数的是( )
| A. | y=x3 | B. | y=2|x| | C. | y=-x2+1 | D. | y=$\frac{1}{x^2}$ |
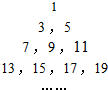 将正奇数排成如图所示的三角形数表:
将正奇数排成如图所示的三角形数表: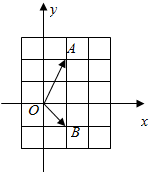 如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )
如图,在复平面内,若复数z1,z2对应的向量分别是$\overrightarrow{{O}{A}}$,$\overrightarrow{{O}{B}}$,则复数z=z1z2-z1-z2-i所对应的点位于( )