题目内容
10．中东呼吸综合征（简称MERS）是由一种新型冠状病毒（MERS-CoV）引起的病毒性呼吸道疾病．截至2015年6月1日，韩国中东呼吸综合征感染者有43人，6月2日，韩国中东呼吸综合征感染者新增2人，3日起每天的新感染者平均比前一天的新感染者增加1人．由于医疗部门采取措施，MERS病毒的传播得到控制，从某天起，每天的新感染者平均比前一天的新感染者减少1人，到6月20日止，MERS的患者共有180人，问6月几日感染MERS的新患者人数最多？并求这一天的新患者人数．分析 由题意，分前后两个时期分别构成等差数列，从而求和可得$\frac{1}{2}$（2+n）（n-1）+$\frac{3}{2}$（20-n）（n-7）=180-43，从而解得．
解答 解：由题意，6月1日到n日，每天新感染者人数构成一数列{an}，
从第二项起，{an}构成等差数列a2=2，d1=1，an=n，
6月2日到n日新增患者$S=\frac{{（{2+n}）（{n-1}）}}{2}$，
从n+1日到20日，每天新感染者人数构成等差数列{bn}，
b1=n-1，d2=-1；
从n+1日到20日，新增患者$T=（{n-1}）（{20-n}）+\frac{1}{2}（{20-n}）（{19-n}）（{-1}）=\frac{3}{2}（{20-n}）（{n-7}）$，
∴S+T=$\frac{1}{2}$（2+n）（n-1）+$\frac{3}{2}$（20-n）（n-7）=180-43，
解得，n=12或n=29（舍去）；
当n=12时，a12=12，
∴6月12日感染MERS的新患者人数最多，为12人．
点评 本题考查了等差数列的应用．
练习册系列答案
阅读快车系列答案
相关题目
1．已知函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为π，且其图象向右平移$\frac{π}{6}$个单位后得到函数g（x）=sin（ωx）的图象，则函数f（x）的图象（ ）
| A． | 关于直线x=$\frac{π}{12}$对称 | B． | 关于直线x=$\frac{5π}{12}$对称 | ||
| C． | 关于点（$\frac{π}{12}$，0）对称 | D． | 关于点（$\frac{5π}{12}$，0）对称 |
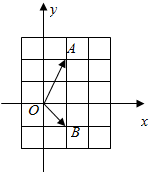如图，在复平面内，若复数z1，z2对应的向量分别是$\overrightarrow{{O}{A}}$，$\overrightarrow{{O}{B}}$，则复数z=z1z2-z1-z2-i所对应的点位于（ ）