题目内容
3．
如图，△ABC为等腰直角三角形，AC=BC=4，∠ACB=90°，D、E分别是边AC和AB的中点，现将△ADE沿DE折起，使平面ADE⊥平面DEBC，H是边AD的中点，平面BCH与AE交于点I．（I）求证：IH∥BC；
（Ⅱ）求多面体HIBCDE的体积．
分析 （Ⅰ）证明ED∥平面BCH，ED∥HI，然后利用平行公理证明IH∥BC．
（Ⅱ）作IM⊥DE，垂足为M，作MN∥DC，交BC于N，则M是DE的中点，利用多面体HIBCDE的体积=VDHC-MIN+VI-EMNB，即可求解体积．
解答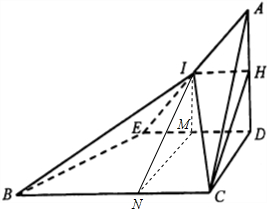 
（Ⅰ）证明：因为D、E分别是边AC和AB的中点，
所以ED∥BC，
因为BC?平面BCH，ED?平面BCH，
所以ED∥平面BCH
因为ED?平面BCH，ED?平面AED，平面BCH∩平面AED=HI
所以ED∥HI
又因为ED∥BC，
所以IH∥BC．
（Ⅱ）解：作IM⊥DE，垂足为M，作MN∥DC，交BC于N，则M是DE的中点，
∴多面体HIBCDE的体积=VDHC-MIN+VI-EMNB=$\frac{1}{2}×2×1×1$+$\frac{1}{3}×\frac{1}{2}×（1+3）×2×1$=1+$\frac{4}{3}$=$\frac{7}{3}$．
点评 本题考查几何体的体积的求法，转化思想的应用，直线与平面平行的判定定理的应用．考查空间想象能力以及计算能力．
练习册系列答案
相关题目
18．执行下面的程序框图，如果输入的N=4，那么输出的S=（ ）
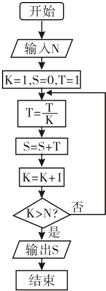
| A． | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ | B． | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$ | ||
| C． | 1+$\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$+$\frac{1}{5}$ | D． | 1+$\frac{1}{2}$+$\frac{1}{3×2}$+$\frac{1}{4×3×2}$+ |
15．下列四个命题：
（1）“?x∈R，2x+5＞0”是全称命题；
（2）命题“?x∈R，x2+5x=6”的否定是“?x0∉R，使x02+5x0≠6”；
（3）若|x|=|y|，则x=y；
（4）若p∨q为假命题，则p、q均为假命题．
其中真命题的序号是（ ）
（1）“?x∈R，2x+5＞0”是全称命题；
（2）命题“?x∈R，x2+5x=6”的否定是“?x0∉R，使x02+5x0≠6”；
（3）若|x|=|y|，则x=y；
（4）若p∨q为假命题，则p、q均为假命题．
其中真命题的序号是（ ）
| A． | （1）（2） | B． | （2）（4） | C． | （1）（4） | D． | （1）（2）（3）（4） |
12．i是虚数单位，若复数z满足iz=3+4i，则z等于（ ）
| A． | 4+3i | B． | 4-3i | C． | -3+4i | D． | -3-4i |
13．在平行四边形ABCD中，点E是BC的中点，$\overrightarrow{BA}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，则$\overrightarrow{DE}$=（ ）
| A． | $\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$ | B． | $\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ | C． | -$\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$ | D． | -$\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ |