题目内容
9.设f-1(x)为f(x)=2x-2+$\frac{x}{2}$,x∈[0,2]的反函数,则y=f(x)+f-1(x)的最大值为4.分析 由f(x)=2x-2+$\frac{x}{2}$在x∈[0,2]上为增函数可得其值域,得到y=f-1(x)在[$\frac{1}{4},2$]上为增函数,由函数的单调性求得y=f(x)+f-1(x)的最大值.
解答 解:由f(x)=2x-2+$\frac{x}{2}$在x∈[0,2]上为增函数,得其值域为[$\frac{1}{4},2$],
可得y=f-1(x)在[$\frac{1}{4},2$]上为增函数,
因此y=f(x)+f-1(x)在[$\frac{1}{4},2$]上为增函数,
∴y=f(x)+f-1(x)的最大值为f(2)+f-1(2)=1+1+2=4.
故答案为:4.
点评 本题考查了互为反函数的两个函数图象间的关系,考查了函数的单调性,属中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
19.设a、b、c分别是△ABC的三边长,且a=4,b=5,c=7,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
20.经过坐标原点,且与圆(x-3)2+(y+1)2=2相切于第四象限的直线方程是( )
| A. | x-y=0 | B. | x+y=0 | C. | x-7y=0 | D. | x+7y=0 |
1.设z1、z2∈C,则“z1、z2均为实数”是“z1-z2是实数”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
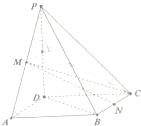 如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为PA、BC的中点,PD⊥平面ABCD,且PD=AD=$\sqrt{2}$,CD=1.