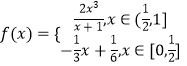��Ŀ����
����Ŀ��ij��Ϊ��ǿ����Ļ���������ʶ������ȫ��������������־Ը�ߣ��ִӷ���������־Ը���������ȡ100����������飺��1��[20��25������2��[25��30������3��[30��35������4��[35��40������5��[40��45]���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
��1�����ӵ�3��4��5�����÷ֲ�����ķ�����ȡ6��־Ը�߲ι㳡���������Ӧ�ӵ�3��4��5�����ȡ������־Ը�ߣ�
��2���ڣ�1���������£����о����ڵ�3��4���־Ը���������ȡ2��־Ը�߽����������飬���4��������һ��־Ը�߱����еĸ��ʣ� 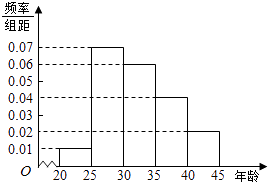
���𰸡�
��1���⣺ ��3�������Ϊ0.3��100=30����4�������Ϊ0.2��100=20����5�������Ϊ0.1��100=10��
��Ϊ��3��4��5�鹲��60��־Ը�ߣ�
�������÷ֲ�����ķ�����60��־Ը���г�ȡ6��־Ը�ߣ�
ÿ���ȡ�������ֱ�Ϊ����3�飺 ![]() ��6=3�� ��4�飺
��6=3�� ��4�飺 ![]() ��6=2�� ��5�飺
��6=2�� ��5�飺 ![]() ��6=1��
��6=1��
����Ӧ�ӵ�3��4��5���зֱ��ȡ3�ˣ�2�ˣ�1�ˣ�
��2���⣺ �ǵ�3���3��־Ը��ΪA1��A2��A3����4���2��־Ը��ΪB1��B2�������5��־Ը���г�ȡ2��־Ը���У�
��A1��A2������A1��A3������A1��B1������A1��B2����
��A2��A3������A2��B1������A2��B2����
��A3��B1������A3��B2������B1��B2������10�֣�
���е�4���2��־Ը��B1��B2������һ��־Ը�߱����е��У�
��A1��B1������A1��B2������A2��B1������A2��B2����
��A3��B1������A3��B2������B1��B2��������7��
���Ե�4��������һ��־Ը�߱����еĸ���Ϊ ![]() ��
��
����������1���ȷֱ������3��������������÷ֲ�����ķ������ɵó��𰸣���2����5��־Ը���г�ȡ2��־Ը����10����������е�4���2��־Ը��B1��B2������һ��־Ը�߱�������7������������ùŵ���͵ĸ��ʼ��㹫ʽ���ɵó���
�����㾫��������Ƶ�ʷֲ�ֱ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��

 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�