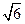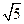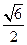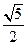题目内容
(本小题满分12分)已知双曲线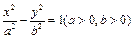 的离心率
的离心率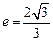 ,过点
,过点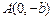 和
和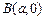 的直线与原点间的距离为
的直线与原点间的距离为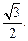
(Ⅰ)求双曲线方程;
(Ⅱ)直线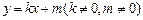 与双曲线交于不同的两点
与双曲线交于不同的两点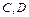 ,且
,且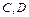 两点都在以
两点都在以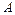 为圆心的同一个圆上,求
为圆心的同一个圆上,求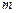 的取值范围.
的取值范围.
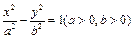 的离心率
的离心率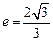 ,过点
,过点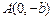 和
和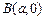 的直线与原点间的距离为
的直线与原点间的距离为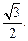
(Ⅰ)求双曲线方程;
(Ⅱ)直线
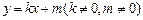 与双曲线交于不同的两点
与双曲线交于不同的两点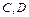 ,且
,且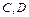 两点都在以
两点都在以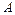 为圆心的同一个圆上,求
为圆心的同一个圆上,求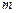 的取值范围.
的取值范围.(Ⅰ)双曲线方程为 .(Ⅱ)
.(Ⅱ)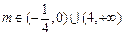
 .(Ⅱ)
.(Ⅱ)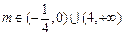
解:(1)设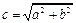 ,
, .
.
整理得AB:bx-ay-ab=0与原点距离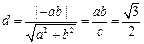 ,又
,又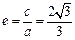 ,
,
联立上式解得b=1,∴c=2, .∴双曲线方程为
.∴双曲线方程为 .
.
(2)设C(x1,y1),D(x2,y2)设CD中点M(x0,y0),
∴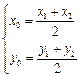 ,∴|AC|=|AD|,∴AM⊥CD.
,∴|AC|=|AD|,∴AM⊥CD.
联立直线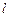 与双曲线的方程得
与双曲线的方程得 ,整理得(1-3k2)x2-6kmx-3m2-3=0,且
,整理得(1-3k2)x2-6kmx-3m2-3=0,且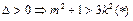 .
.
∴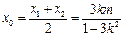 ,
, 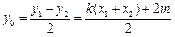 ,
,
∴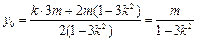 ∴
∴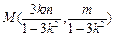 ,∴AM⊥CD.
,∴AM⊥CD.
∴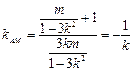 ,整理得
,整理得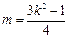 ,
,
则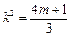 且k2>0,,代入
且k2>0,,代入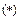 中得
中得 .
.
∴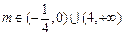 .
.
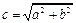 ,
, .
.整理得AB:bx-ay-ab=0与原点距离
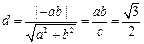 ,又
,又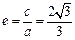 ,
,联立上式解得b=1,∴c=2,
 .∴双曲线方程为
.∴双曲线方程为 .
.(2)设C(x1,y1),D(x2,y2)设CD中点M(x0,y0),
∴
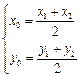 ,∴|AC|=|AD|,∴AM⊥CD.
,∴|AC|=|AD|,∴AM⊥CD.联立直线
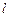 与双曲线的方程得
与双曲线的方程得 ,整理得(1-3k2)x2-6kmx-3m2-3=0,且
,整理得(1-3k2)x2-6kmx-3m2-3=0,且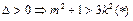 .
.∴
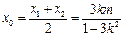 ,
, 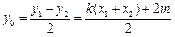 ,
,∴
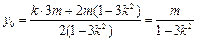 ∴
∴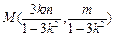 ,∴AM⊥CD.
,∴AM⊥CD.∴
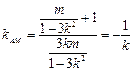 ,整理得
,整理得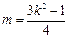 ,
,则
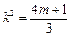 且k2>0,,代入
且k2>0,,代入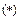 中得
中得 .
.∴
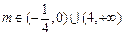 .
.
练习册系列答案
相关题目
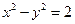 的右焦点为
的右焦点为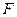 ,过点
,过点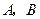 两点,点
两点,点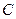 的坐标是
的坐标是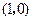 .
.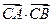 为常数;
为常数;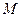 满足
满足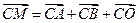 (其中
(其中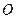 为坐标原点),求点
为坐标原点),求点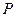 到点
到点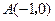 和
和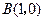 的距离分别为
的距离分别为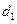 和
和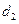 ,
,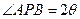 ,且存在常数
,且存在常数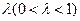 ,使得
,使得
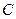 为双曲线,并求出
为双曲线,并求出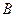 作直线交双曲线
作直线交双曲线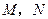 两点,试确定
两点,试确定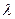 的范围,使
的范围,使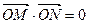 ,其中点
,其中点 为坐标原点
为坐标原点 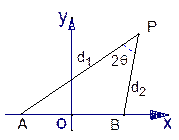
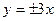 ,它的一个焦点是
,它的一个焦点是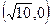 ,则双曲线的方程是__________.
,则双曲线的方程是__________.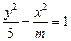 的渐近线方程为
的渐近线方程为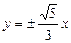 ,则双曲线焦点F到渐近线的距离为
,则双曲线焦点F到渐近线的距离为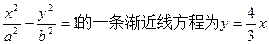 ,
,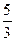
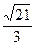
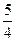
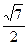
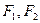 为双曲线
为双曲线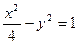 的两个焦点,点
的两个焦点,点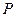 在双曲线上且满足
在双曲线上且满足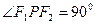 ,则
,则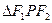 的面积是____________________
的面积是____________________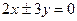 ,且过点
,且过点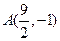 ,求双曲线的标准方程。
,求双曲线的标准方程。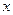 轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为
轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为