题目内容
(文科)已知双曲线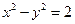 的右焦点为
的右焦点为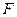 ,过点
,过点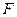 的动直线与双曲线相交于
的动直线与双曲线相交于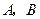 两点,点
两点,点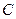 的坐标是
的坐标是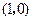 .
.
(I)证明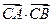 为常数;
为常数;
(II)若动点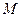 满足
满足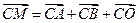 (其中
(其中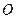 为坐标原点),求点
为坐标原点),求点 的轨迹方程.
的轨迹方程.
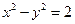 的右焦点为
的右焦点为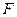 ,过点
,过点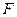 的动直线与双曲线相交于
的动直线与双曲线相交于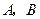 两点,点
两点,点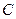 的坐标是
的坐标是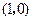 .
.(I)证明
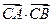 为常数;
为常数;(II)若动点
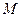 满足
满足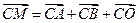 (其中
(其中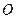 为坐标原点),求点
为坐标原点),求点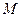 的轨迹方程.
的轨迹方程.(1)略
(2)
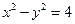
(文科)解:由条件知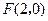 ,设
,设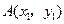 ,
,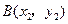 .
.
(I)当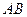 与
与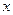 轴垂直时,可设点
轴垂直时,可设点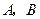 的坐标分别为
的坐标分别为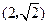 ,
,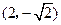 ,
,
此时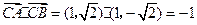 .
.
当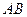 不与
不与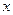 轴垂直时,设直线
轴垂直时,设直线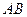 的方程是
的方程是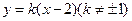 .
.
代入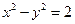 ,有
,有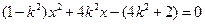 .
.
则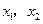 是上述方程的两个实根,所以
是上述方程的两个实根,所以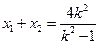 ,
,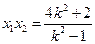 ,
,
于是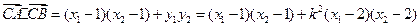
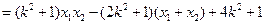
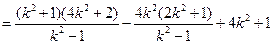
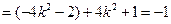 .综上所述,
.综上所述,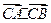 为常数
为常数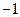 .
.
(II)解法一:设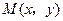 ,则
,则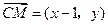 ,
,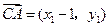 ,
,
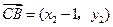 ,
,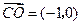 ,由
,由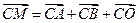 得:
得:
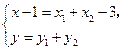 即
即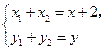 于是
于是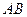 的中点坐标为
的中点坐标为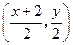 .
.
当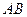 不与
不与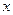 轴垂直时,
轴垂直时,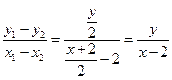 ,即
,即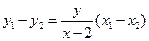 .
.
又因为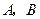 两点在双曲线上,所以
两点在双曲线上,所以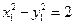 ,
,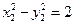 ,两式相减得
,两式相减得
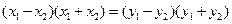 ,即
,即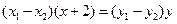 .
.
将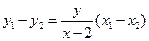 代入上式,化简得
代入上式,化简得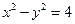 .
.
当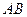 与
与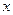 轴垂直时,
轴垂直时,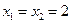 ,求得
,求得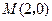 ,也满足上述方程.
,也满足上述方程.
所以点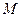 的轨迹方程是
的轨迹方程是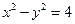 .
.
解法二:同解法一得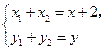 ……………………………………①
……………………………………①
当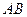 不与
不与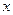 轴垂直时,由(I)有
轴垂直时,由(I)有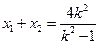 .…………………②
.…………………②
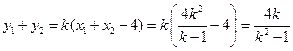 .………………………③
.………………………③
由①、②、③得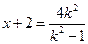 . …④
. …④ 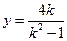 .…⑤
.…⑤
当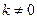 时,
时,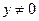 ,由④、⑤得,
,由④、⑤得,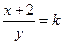 ,将其代入⑤有
,将其代入⑤有
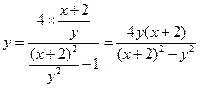 .整理得
.整理得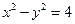 .
.
当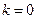 时,点
时,点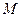 的坐标为
的坐标为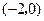 ,满足上述方程.
,满足上述方程.
当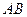 与
与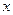 轴垂直时,
轴垂直时,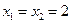 ,求得
,求得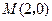 ,也满足上述方程.
,也满足上述方程.
故点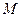 的轨迹方程是
的轨迹方程是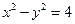 .
.
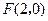 ,设
,设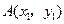 ,
,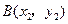 .
.(I)当
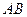 与
与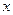 轴垂直时,可设点
轴垂直时,可设点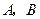 的坐标分别为
的坐标分别为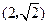 ,
,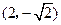 ,
,此时
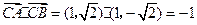 .
.当
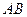 不与
不与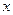 轴垂直时,设直线
轴垂直时,设直线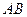 的方程是
的方程是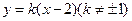 .
.代入
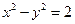 ,有
,有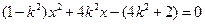 .
.则
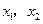 是上述方程的两个实根,所以
是上述方程的两个实根,所以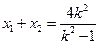 ,
,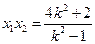 ,
,于是
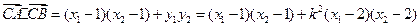
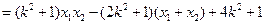
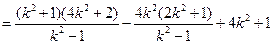
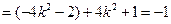 .综上所述,
.综上所述,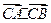 为常数
为常数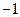 .
.(II)解法一:设
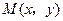 ,则
,则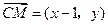 ,
,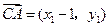 ,
,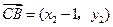 ,
,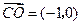 ,由
,由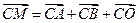 得:
得: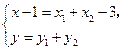 即
即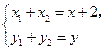 于是
于是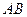 的中点坐标为
的中点坐标为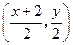 .
.当
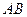 不与
不与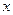 轴垂直时,
轴垂直时,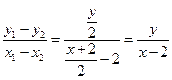 ,即
,即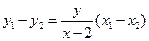 .
.又因为
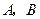 两点在双曲线上,所以
两点在双曲线上,所以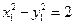 ,
,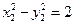 ,两式相减得
,两式相减得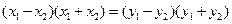 ,即
,即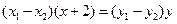 .
.将
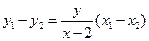 代入上式,化简得
代入上式,化简得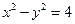 .
.当
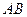 与
与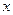 轴垂直时,
轴垂直时,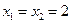 ,求得
,求得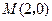 ,也满足上述方程.
,也满足上述方程.所以点
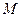 的轨迹方程是
的轨迹方程是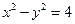 .
.解法二:同解法一得
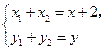 ……………………………………①
……………………………………①当
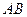 不与
不与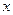 轴垂直时,由(I)有
轴垂直时,由(I)有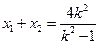 .…………………②
.…………………②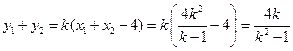 .………………………③
.………………………③由①、②、③得
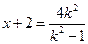 . …④
. …④ 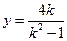 .…⑤
.…⑤当
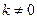 时,
时,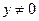 ,由④、⑤得,
,由④、⑤得,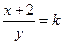 ,将其代入⑤有
,将其代入⑤有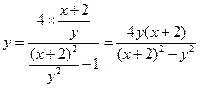 .整理得
.整理得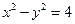 .
.当
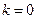 时,点
时,点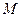 的坐标为
的坐标为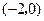 ,满足上述方程.
,满足上述方程.当
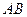 与
与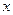 轴垂直时,
轴垂直时,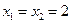 ,求得
,求得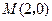 ,也满足上述方程.
,也满足上述方程.故点
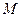 的轨迹方程是
的轨迹方程是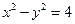 .
.
练习册系列答案
相关题目
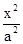 -
-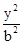 =1(a>0,b>0)的一条渐近线方程为y=x,则有
=1(a>0,b>0)的一条渐近线方程为y=x,则有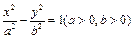 的离心率
的离心率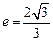 ,过点
,过点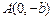 和
和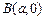 的直线与原点间的距离为
的直线与原点间的距离为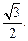
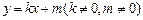 与双曲线交于不同的两点
与双曲线交于不同的两点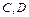 ,且
,且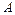 为圆心的同一个圆上,求
为圆心的同一个圆上,求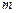 的取值范围.
的取值范围.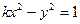 的一条渐近线与直线
的一条渐近线与直线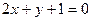 垂直,那么双曲线的离心 率为 ;渐近线方程为
垂直,那么双曲线的离心 率为 ;渐近线方程为 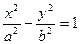 的渐近线与圆
的渐近线与圆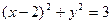 相切,则此双曲线的离心率为________
相切,则此双曲线的离心率为________ 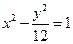 上的一点,
上的一点,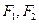 是该双曲线的两个焦点,若
是该双曲线的两个焦点,若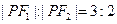 ,则
,则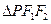 的面积为___________.
的面积为___________.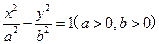 的离心率
的离心率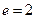 ,则其渐近线的方程为 .
,则其渐近线的方程为 .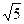
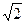
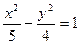 有且只有一个公共点的直线共有
有且只有一个公共点的直线共有  条.
条.