题目内容
直线 过抛物线
过抛物线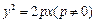 的焦点,并且与抛物线相交于
的焦点,并且与抛物线相交于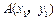 和
和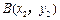 两点
两点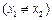 .求证:对于此抛物线的任意给定的一条弦
.求证:对于此抛物线的任意给定的一条弦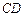 ,直线
,直线 不是
不是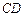 的垂直平分线.用反证法证明.
的垂直平分线.用反证法证明.
 过抛物线
过抛物线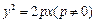 的焦点,并且与抛物线相交于
的焦点,并且与抛物线相交于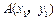 和
和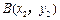 两点
两点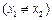 .求证:对于此抛物线的任意给定的一条弦
.求证:对于此抛物线的任意给定的一条弦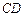 ,直线
,直线 不是
不是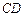 的垂直平分线.用反证法证明.
的垂直平分线.用反证法证明. 证明见解析
证明:假设直线 是
是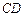 的垂直平分线,设
的垂直平分线,设 的斜率为
的斜率为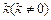 ,则
,则 的方程是
的方程是 .
.
设直线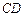 与
与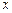 轴的交点坐标为
轴的交点坐标为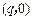 ,则
,则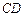 的方程是
的方程是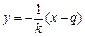 .
.
设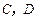 的坐标分别为
的坐标分别为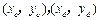 ,则
,则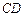 的中点坐标是
的中点坐标是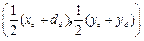 .
.
可知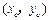 ,
,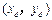 是方程组
是方程组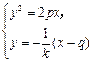 的两组解.
的两组解.
方程组消去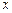 ,得
,得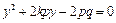 . ①
. ①
显然,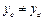 ,方程①有两个不等的实数根,故
,方程①有两个不等的实数根,故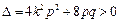 ,
,
于是有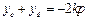 ,
,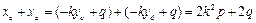 .
.
但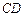 的中点坐标满足方程
的中点坐标满足方程 ,
,
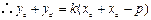 ,
,
即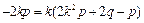 ,
,
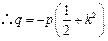 .
.
因此有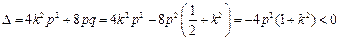 ,
,
这与①式中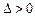 矛盾,原假定不成立.
矛盾,原假定不成立.
所以,直线 不是
不是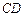 的垂直平分线.
的垂直平分线.
 是
是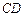 的垂直平分线,设
的垂直平分线,设 的斜率为
的斜率为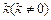 ,则
,则 的方程是
的方程是 .
.设直线
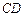 与
与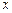 轴的交点坐标为
轴的交点坐标为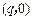 ,则
,则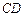 的方程是
的方程是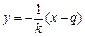 .
.设
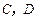 的坐标分别为
的坐标分别为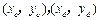 ,则
,则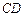 的中点坐标是
的中点坐标是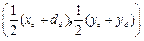 .
.可知
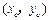 ,
,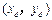 是方程组
是方程组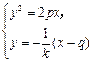 的两组解.
的两组解.方程组消去
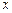 ,得
,得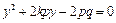 . ①
. ①显然,
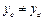 ,方程①有两个不等的实数根,故
,方程①有两个不等的实数根,故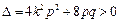 ,
,于是有
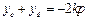 ,
,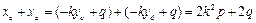 .
.但
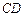 的中点坐标满足方程
的中点坐标满足方程 ,
,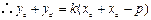 ,
,即
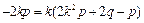 ,
,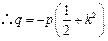 .
.因此有
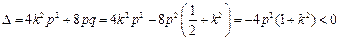 ,
,这与①式中
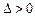 矛盾,原假定不成立.
矛盾,原假定不成立.所以,直线
 不是
不是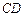 的垂直平分线.
的垂直平分线.
练习册系列答案
相关题目
 的倒数成等差数列,求证:角
的倒数成等差数列,求证:角
 .
.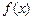 在
在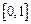 上有意义,且
上有意义,且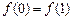 ,如果对于不同的
,如果对于不同的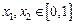 ,都有
,都有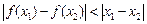 ,求证:
,求证: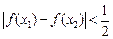 。那么他的反设应该是___________.
。那么他的反设应该是___________. 满足
满足 (
( 为虚数单位),则
为虚数单位),则 为 .
为 . 为正整数,用数学归纳法证明
为正整数,用数学归纳法证明
 时,若已假设
时,若已假设 (
( 为偶数)真,则还需利用归纳假设再证( )
为偶数)真,则还需利用归纳假设再证( ) 时等式也成立 B
时等式也成立 B 、
、 时等式也成立
时等式也成立  时等式也成立 D、
时等式也成立 D、 时等式也成立
时等式也成立 都是偶数”,正确的反设为(***)
都是偶数”,正确的反设为(***)