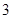题目内容
已知：a、b、c是互不相等的非零实数.
求证：三个方程ax2+2bx+c=0，bx2+2cx+a=0，cx2+2ax+b=0至少有一个方程有两个相异实根.
求证：三个方程ax2+2bx+c=0，bx2+2cx+a=0，cx2+2ax+b=0至少有一个方程有两个相异实根.
证明略
（反证法）：假设三个方程中都没有两个相异实根，
则Δ1=4b2－4ac≤0，Δ2=4c2－4ab≤0，Δ3=4a2－4bc≤0.
相加有a2－2ab+b2+b2－2bc+c2+c2－2ac+a2≤0，
（a－b）2+（b－c）2+（c－a）2≤0. ①
由题意a、b、c互不相等，∴①式不能成立.
∴假设不成立，即三个方程中至少有一个方程有两个相异实根.
则Δ1=4b2－4ac≤0，Δ2=4c2－4ab≤0，Δ3=4a2－4bc≤0.
相加有a2－2ab+b2+b2－2bc+c2+c2－2ac+a2≤0，
（a－b）2+（b－c）2+（c－a）2≤0. ①
由题意a、b、c互不相等，∴①式不能成立.
∴假设不成立，即三个方程中至少有一个方程有两个相异实根.
练习册系列答案
备战中考寒假系列答案
相关题目
过抛物线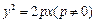
的焦点，并且与抛物线相交于
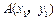和
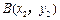两点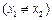
.求证：对于此抛物线的任意给定的一条弦
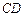，直线
且
，求证：
为正整数，且
与
皆为完全平方数，对于以下两个命题：
必为合数；（乙）.
必为两个平方数的和.
为纯虚数，则实数
值为（ ）
