题目内容
证明：在复数范围内，方程
（
为虚数单位）无解．
假设存在这样的复数，原方程化简为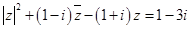
设
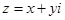代入得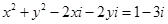
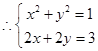方程组无实数解∴假设不成立，即原方程在复数范围内无解
解析试题分析：假设存在这样的复数，则
原方程化简为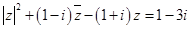
设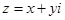代入上述方程得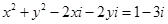 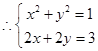方程组无实数解
∴假设不成立，即原方程在复数范围内无解.
考点：反证法及复数运算
点评：当直接证明不易时考虑反证法，先假设所要证明的反面成立，借此来推出矛盾，从而肯定原结论成立
练习册系列答案
相关题目
题目内容
证明：在复数范围内，方程（为虚数单位）无解．
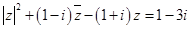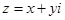假设存在这样的复数，原方程化简为设代入得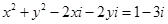 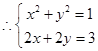方程组无实数解∴假设不成立，即原方程在复数范围内无解
解析试题分析：假设存在这样的复数，则
原方程化简为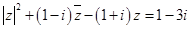
设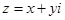代入上述方程得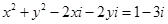 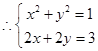方程组无实数解
∴假设不成立，即原方程在复数范围内无解.
考点：反证法及复数运算
点评：当直接证明不易时考虑反证法，先假设所要证明的反面成立，借此来推出矛盾，从而肯定原结论成立
，（
，
为虚单位）。
为实数，求
的值；
.?
(
),
是实数，
是虚数单位.
所表示的点在第一象限，求实数m的取值范围.
是
（
）
是实数，求
的值；
内，
,当实数
为何值时,
为实数; 
纯虚数.