ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋÄģŅ§ÐĢΊÁË―âąūÐĢÎÄĄĒĀíŋÆŅ§ÉúĩÄŅ§ŌĩËŪÆ―ÄĢÄâēâĘÔĘýŅ§ģÉžĻĮéŋöĢŽ·ÖąðīÓĀíŋÆ°āŅ§ÉúÖÐËæŧúģéČĄ![]() ČËĩÄģÉžĻĩÃĩ―ŅųąūžŨĢŽīÓÎÄŋÆ°āŅ§ÉúÖÐËæŧúģéČĄ
ČËĩÄģÉžĻĩÃĩ―ŅųąūžŨĢŽīÓÎÄŋÆ°āŅ§ÉúÖÐËæŧúģéČĄ![]() ČËĩÄģÉžĻĩÃĩ―ŅųąūŌŌĢŽļųūÝÁ―ļöŅųąūĘýūÝ·ÖąðĩÃĩ―ČįÏÂÖą·―ÍžĢš
ČËĩÄģÉžĻĩÃĩ―ŅųąūŌŌĢŽļųūÝÁ―ļöŅųąūĘýūÝ·ÖąðĩÃĩ―ČįÏÂÖą·―ÍžĢš
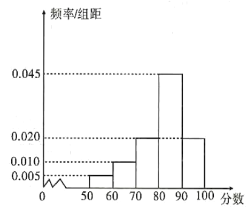
žŨŅųąūĘýūÝÖą·―Íž
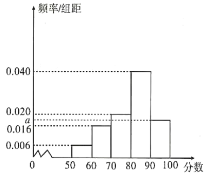
ŌŌŅųąūĘýūÝÖą·―Íž
ŌŅÖŠŌŌŅųąūÖÐĘýūÝÔÚ![]() ĩÄÓÐ
ĩÄÓÐ![]() ļö.
ļö.
ĢĻ1ĢĐĮó![]() šÍŌŌŅųąūÖą·―ÍžÖÐ
šÍŌŌŅųąūÖą·―ÍžÖÐ![]() ĩÄÖĩĢŧ
ĩÄÖĩĢŧ
ĢĻ2ĢĐĘÔđĀžÆļÃÐĢĀíŋÆ°āŅ§ÉúąūīÎÄĢÄâēâĘÔĘýŅ§ģÉžĻĩÄÆ―ūųÖĩšÍÎÄŋÆ°āŅ§ÉúąūīÎÄĢÄâēâĘÔĘýŅ§ģÉžĻĩÄÖÐÎŧĘýĢĻÍŽŌŧŨéÖÐĩÄĘýūÝÓÃļÃŨéĮøžäÖÐĩãÖĩΊīúąíĢĐ.
Ąūīð°ļĄŋĢĻ1ĢĐ![]() ĢŽ
ĢŽ![]() Ģŧ
Ģŧ
ĢĻ2ĢĐ81.5,82.5.
Ąū―âÎöĄŋ
ĢĻ1ĢĐĘŨÏČžÆËãŌŌŅųąūÖÐĘýūÝÔÚ![]() ĩÄÆĩÂĘĢŽČŧšóžÆËãŅųąūČÝÁŋĢŽĀûÓÃÆĩÂĘšÍĩČÓÚ1Įó
ĩÄÆĩÂĘĢŽČŧšóžÆËãŅųąūČÝÁŋĢŽĀûÓÃÆĩÂĘšÍĩČÓÚ1Įó![]() ĢŧĢĻ2ĢĐļųūÝŅųąūÆ―ūųÖĩšÍÖÐÎŧĘýĩÄžÆËãđŦĘ―·ÖąðžÆËãĢŧ
ĢŧĢĻ2ĢĐļųūÝŅųąūÆ―ūųÖĩšÍÖÐÎŧĘýĩÄžÆËãđŦĘ―·ÖąðžÆËãĢŧ
ĢĻ1ĢĐÓÉÖą·―ÍžŋÉÖŠĢŽŌŌŅųąūÖÐĘýūÝÔÚ![]() ĩÄÆĩÂĘΊ
ĩÄÆĩÂĘΊ![]() ĢŽķøÕâļöŨéŅ§ÉúÓÐ
ĢŽķøÕâļöŨéŅ§ÉúÓÐ![]() ČËĢŽÔō
ČËĢŽÔō![]() ĢŽĩÃ
ĢŽĩÃ![]() .
.
ÓÉŌŌŅųąūĘýūÝÖą·―ÍžŋÉÖŠ![]() ĢŽ
ĢŽ
đĘ![]() .
.
ĢĻ2ĢĐžŨŅųąūĘýūÝĩÄÆ―ūųÖĩđĀžÆÖĩΊ
![]() .
.
ÓÉĢĻ1ĢĐÖŠ![]() ĢŽđĘŌŌŅųąūĘýūÝÖą·―ÍžÖÐĮ°ČýŨéĩÄÆĩÂĘÖŪšÍΊ
ĢŽđĘŌŌŅųąūĘýūÝÖą·―ÍžÖÐĮ°ČýŨéĩÄÆĩÂĘÖŪšÍΊ
![]() ĢŽ
ĢŽ
Į°ËÄŨéĩÄÆĩÂĘÖŪšÍΊ![]() ĢŽ
ĢŽ
đĘŌŌŅųąūĘýūÝĩÄÖÐÎŧĘýÔÚĩÚ![]() ŨéĢŽÔōŋÉÉčļÃÖÐÎŧĘýΊ
ŨéĢŽÔōŋÉÉčļÃÖÐÎŧĘýΊ![]() ĢŽ
ĢŽ
ÓÉ![]() ĩÃ
ĩÃ
![]() ĢŽđĘŌŌŅųąūĘýūÝĩÄÖÐÎŧĘýΊ
ĢŽđĘŌŌŅųąūĘýūÝĩÄÖÐÎŧĘýΊ![]() .
.
ļųūÝŅųąūđĀžÆŨÜĖåĩÄËžÏëĢŽŋÉŌÔđĀžÆļÃÐĢĀíŋÆ°āŅ§ÉúąūīÎÄĢÄâēâĘÔĘýŅ§ģÉžĻĩÄÆ―ūųÖĩԞΊ![]() ĢŽÎÄŋÆ°āŅ§ÉúąūīÎÄĢÄâēâĘÔĘýŅ§ģÉžĻĩÄÖÐÎŧĘýԞΊ
ĢŽÎÄŋÆ°āŅ§ÉúąūīÎÄĢÄâēâĘÔĘýŅ§ģÉžĻĩÄÖÐÎŧĘýԞΊ![]() .
.

 ÃûÐĢŋÎĖÃÏĩÁÐīð°ļ
ÃûÐĢŋÎĖÃÏĩÁÐīð°ļĄūĖâÄŋĄŋŌŧŅÐŅ§ĘĩžųŧîķŊÐĄŨéĀûÓÃŋÎÓāĘąžäĢŽķÔÄģđŦËū1Ô·ÝÖÁ5Ô·ÝÏúĘÛÄģÖÖēúÆ·ĩÄÏúĘÛÁŋž°ÏúĘÛĩĨžÛ―øÐÐÁËĩũēéĢŽÔÂÏúĘÛĩĨžÛ![]() ĢĻĩĨÎŧĢšÔŠĢĐšÍÔÂÏúĘÛÁŋ
ĢĻĩĨÎŧĢšÔŠĢĐšÍÔÂÏúĘÛÁŋ![]() ĢĻĩĨÎŧĢš°ŲžþĢĐÖŪžäĩÄŌŧŨéĘýūÝČįÏÂąíËųĘūĢš
ĢĻĩĨÎŧĢš°ŲžþĢĐÖŪžäĩÄŌŧŨéĘýūÝČįÏÂąíËųĘūĢš
ÔÂ·Ý | 1 | 2 | 3 | 4 | 5 |
ÔÂÏúĘÛĩĨžÛ | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
ÔÂÏúĘÛÁŋ | 10 | 8 | 7 | 6 | 4 |
ĢĻ1ĢĐļųūÝ1ÖÁ5Ô·ÝĩÄĘýūÝĢŽĮóģö![]() đØÓÚ
đØÓÚ![]() ĩÄŧØđéÖąÏß·―ģĖĢŧ
ĩÄŧØđéÖąÏß·―ģĖĢŧ
ĢĻ2ĢĐÔĪžÆÔÚ―ņšóĩÄÏúĘÛÖÐĢŽÔÂÏúĘÛÁŋÓëÔÂÏúĘÛĩĨžÛČÔČŧ·þīÓĢĻ1ĢĐÖÐĩÄđØÏĩĢŽČôļÃÖÖēúÆ·ĩÄģÉąūĘĮ1ÔŠ/žþĢŽÄĮÃīļÃēúÆ·ĩÄÔÂÏúĘÛĩĨžÛÓĶķĻΊķāÉŲÔŠēÅÄÜŧņĩÃŨîīóÔÂĀûČóĢŋĢĻŨĒĢšĀûČó=ÏúĘÛĘÕČë-ģÉąūĢĐ
ĢĻŧØđéÖąÏß·―ģĖ![]() ĢŽÆäÖÐ
ĢŽÆäÖÐ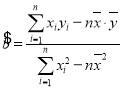 .ēÎŋžĘýūÝĢš
.ēÎŋžĘýūÝĢš![]() ĢŽ
ĢŽ![]() ĢĐ
ĢĐ