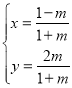题目内容
【题目】一研学实践活动小组利用课余时间,对某公司1月份至5月份销售某种产品的销售量及销售单价进行了调查,月销售单价![]() (单位:元)和月销售量
(单位:元)和月销售量![]() (单位:百件)之间的一组数据如下表所示:
(单位:百件)之间的一组数据如下表所示:
月份 | 1 | 2 | 3 | 4 | 5 |
月销售单价 | 1.6 | 1.8 | 2 | 2.2 | 2.4 |
月销售量 | 10 | 8 | 7 | 6 | 4 |
(1)根据1至5月份的数据,求出![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)预计在今后的销售中,月销售量与月销售单价仍然服从(1)中的关系,若该种产品的成本是1元/件,那么该产品的月销售单价应定为多少元才能获得最大月利润?(注:利润=销售收入-成本)
(回归直线方程![]() ,其中
,其中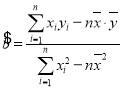 .参考数据:
.参考数据:![]() ,
,![]() )
)
【答案】(1)回归直线方程为![]() (2)该产品的月销售单价应定为2元才能获得最大月利润
(2)该产品的月销售单价应定为2元才能获得最大月利润
【解析】
(1)分别求出![]() ,再结合提供的数据和公式求出
,再结合提供的数据和公式求出![]() ,即可求出回归直线方程;
,即可求出回归直线方程;
(2)根据(1)中的回归直线方程,可得当定价为![]() 时的销售量
时的销售量![]() ,列出利润
,列出利润![]() 的函数
的函数![]() ,求二次函数的最值,即可求解.
,求二次函数的最值,即可求解.
解:(1)∵![]() ,
,![]() .
.
∴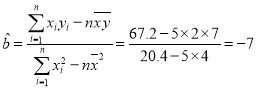 .
.
![]() .
.
∴回归直线方程为![]() .
.
(2)设该产品的月销售单价为![]() 元,月利润为
元,月利润为![]() 百元,则
百元,则
∵![]() ,
,
∴![]()
![]() .
.
∴当![]() 时,
时,![]() (百元).
(百元).
∴该产品的月销售单价应定为2元才能获得最大月利润为7百元.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目