题目内容
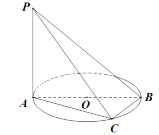
【题目】已知C是以AB为直径的圆周上一点,![]() 平面
平面![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若异面直线PB与AC所成的为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由线面垂直的性质定理可知![]() .再由
.再由![]() 以及线面垂直的判断定理,可知
以及线面垂直的判断定理,可知![]() 平面
平面![]() ,即可证明.
,即可证明.
(2)解法1,建立空间直角坐标系,令![]() ,确定点坐标,令
,确定点坐标,令![]()
![]() ,由题意可知
,由题意可知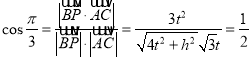 ,即
,即![]() ,再求平面
,再求平面![]() 的法向量为
的法向量为![]() 与平面
与平面![]() 的法向量为
的法向量为![]() ,求解
,求解![]() 即可.解法2:过
即可.解法2:过![]() 作
作![]() 的平行线
的平行线![]() 交圆于
交圆于![]() ,连接
,连接![]() ,
,![]() ,所以直线
,所以直线![]() 与
与![]() 所成的角,即为
所成的角,即为![]() 与
与![]() 所成的角,
所成的角,![]() ,再过
,再过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,由三垂线定理知
,由三垂线定理知![]() ,所以
,所以![]() 即为二面角
即为二面角![]() 的平面角,求解边长即可.
的平面角,求解边长即可.
(1)证明:因为![]() 为圆的直径,所以
为圆的直径,所以![]() ,
,
又![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() ,
,
而![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() 平面
平面![]() ;
;
(2)解法1:建系如图所示
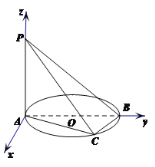
令![]() ,而
,而![]() ,则
,则![]() ,
,![]() .
.
则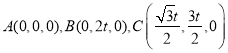 ,令
,令![]()
![]()
所以![]() ,
,![]() .
.
因为异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
故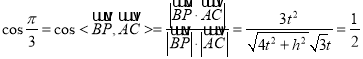 ,解得
,解得![]() .
.
令平面![]() 的一个法向量为
的一个法向量为![]()
而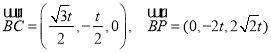
由![]()
![]() ,
,![]() ,所以
,所以![]()
由![]() ,
,![]() ,所以
,所以![]() ,即
,即![]()
而平面![]() 的一个法向量为
的一个法向量为![]()
所以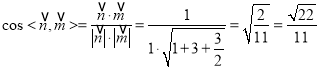 .
.
所以二面角![]() 的余弦值为
的余弦值为![]()
解法2:过![]() 作
作![]() 的平行线
的平行线![]() 交圆于
交圆于![]() ,连接
,连接![]() ,
,![]()
所以直线![]() 与
与![]() 所成的角,即为
所成的角,即为![]() 与
与![]() 所成的角.
所成的角.
因为![]() 为圆的直径,所以
为圆的直径,所以![]()
又![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() 平面
平面![]()
而![]() 平面
平面![]() ,所以
,所以![]() ,则
,则![]() .
.
令![]() ,且
,且![]() 所以
所以![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
过![]() 作
作![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,由三垂线定理知
,由三垂线定理知![]() .
.
所以![]() 即为二面角
即为二面角![]() 的平面角.
的平面角.
![]() ,
,![]()
![]() 即
即 ![]() .
.
即为二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】某市在争创文明城市过程中,为调查市民对文明出行机动车礼让行人的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于45岁 | 80 | ||
年龄大于45岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄段与是否支持文明出行机动车礼让行人有关?
(3)已知在被调查的年龄小于25岁的支持者有5人,其中2人是教师,现从这5人中随机抽取3人,求至多抽到1位教师的概率.