题目内容
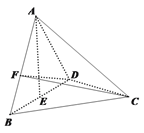
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一动点,记
上一动点,记![]() .
.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】分析:(1)建立空间直角坐标系,设立各点坐标,根据向量数量积求向量夹角,最后根据线线角与向量夹角相等或互补得结果,(2)建立空间直角坐标系,设立各点坐标,利用方程组求平面![]() 的一个法向量,再根据向量数量积求向量夹角,最后根据线面角与向量夹角互余列等量关系,解得结果,
的一个法向量,再根据向量数量积求向量夹角,最后根据线面角与向量夹角互余列等量关系,解得结果,
详解:连接CE, 以![]() 分别为
分别为![]() 轴,
轴,
建立如图空间直角坐标系,
则![]() ,
,
因为F为线段AB上一动点,且![]() ,
,
则![]() , 所以
, 所以![]() .
.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
所以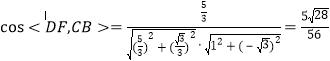 .
.
(2)![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() =
=![]()
由![]()
![]() ,
,![]()
![]() 得
得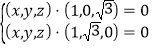 ,化简得
,化简得![]() ,取
,取![]()
![]()
设与平面
![]() 所成角为
所成角为![]() ,
,
则![]() .
.
解得![]() 或
或![]() (舍去),所以
(舍去),所以![]() .
.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目

