题目内容
【题目】已知定义域为![]() 的单调减函数
的单调减函数![]() 是奇函数,当
是奇函数,当![]() 时,
时,![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求![]() 的解析式;
的解析式;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)
;(II)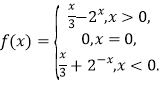 ;(III)
;(III)![]() .
.
【解析】
(Ⅰ)利用定义域为R的函数f(x)是奇函数,求f(0)的值;
(Ⅱ)求出x<0的解析式,即可求f(x)的解析式;
(Ⅲ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,f(x)在R上是减函数,所以t2﹣2t>k﹣2t2.即3t2﹣2t﹣k>0对任意t∈R恒成立,利用判别式小于0即可求实数k的取值范围.
(Ⅰ)因为定义域为![]() 的函数
的函数![]() 是奇函数,
是奇函数,
所以![]() .
.
(Ⅱ)因为当![]() 时,
时,![]() ,
,
所以![]() .
.
又因为函数![]() 是奇函数,所以
是奇函数,所以![]() .
.
所以![]() .
.
综上,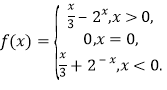
(Ⅲ)由![]() 得
得![]() .
.
因为![]() 是奇函数,
是奇函数,
所以![]() .
.
又![]() 在
在![]() 上是减函数,所以
上是减函数,所以![]() .
.
即![]() 对任意
对任意![]() 恒成立.
恒成立.
令![]() ,则
,则![]() .由
.由![]() ,解得
,解得![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目