题目内容
【题目】设函数![]() ,已知曲线
,已知曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行
平行
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)是否存在自然数![]() ,使得方程
,使得方程![]() 在
在![]() 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出![]() ;如果不存在,请说明理由。
;如果不存在,请说明理由。
(Ⅲ)设函数![]() (
(![]() 表示
表示![]() 中的较小者),求
中的较小者),求![]() 的最大值。
的最大值。
【答案】(1) ![]() .
.
(2) ![]() 时,方程
时,方程![]() 在
在![]() 内存在唯一的根.证明见解析.
内存在唯一的根.证明见解析.
(3) ![]() .
.
【解析】试题分析:(Ⅰ)求出f(x)的导数,求得切线的斜率,由两直线平行的条件:斜率相等,解方程可得![]() ;(Ⅱ)求出
;(Ⅱ)求出![]() 的导数和单调区间,最值,由零点存在定理,即可判断存在
的导数和单调区间,最值,由零点存在定理,即可判断存在![]() ;(Ⅲ)由(Ⅱ)求得
;(Ⅲ)由(Ⅱ)求得![]() 的解析式,通过
的解析式,通过![]() 的最大值,即可得到所求.
的最大值,即可得到所求.
试题解析:(Ⅰ)由题意知,曲线![]() 在点
在点![]() 处的切线斜率为
处的切线斜率为![]() ,所以
,所以![]() ,
,
又![]() 所以
所以![]() .
.
(Ⅱ)![]() 时,方程
时,方程![]() 在
在![]() 内存在唯一的根.
内存在唯一的根.
设![]()
当![]() 时,
时, ![]() .
.
又![]()
所以存在![]() ,使
,使![]() .
.
因为![]() 所以当
所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以当![]() 时,
时, ![]() 单调递增.
单调递增.
所以![]() 时,方程
时,方程![]() 在
在![]() 内存在唯一的根.
内存在唯一的根.
(Ⅲ)由(Ⅱ)知,方程![]() 在
在![]() 内存在唯一的根
内存在唯一的根![]() ,且
,且![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() ,所以
,所以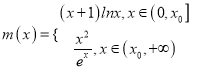 .
.
当![]() 时,若
时,若![]()
若![]() 由
由![]() 可知
可知![]() 故
故![]()
当![]() 时,由
时,由![]() 可得
可得![]() 时,
时, ![]() 单调递增;
单调递增; ![]() 时,
时, ![]() 单调递减;
单调递减;
可知![]() 且
且![]() .
.
综上可得函数![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目
【题目】某校的学生文娱团队由理科组和文科组构成,具体数据如表所示:
组别 | 文科 | 理科 | ||
性别 | 男生 | 女生 | 男生 | 女生 |
人数 | 3 | 1 | 3 | 2 |
学校准备从该文娱团队中选出4人到某社区参加大型公益活动演出,每选出一名男生,给其所在的组记1分;每选出一名女生,给其所在的组记2分,要求被选出的4人中文科组和理科组的学生都有.
(I)求理科组恰好得4分的概率;
(II)记文科组的得分为X,求随机变量X的分布列和数学期望EX.