Question

11．设四边形ABCD为平行四边形，|$\overrightarrow{AB}$|=6，|$\overrightarrow{AD}$|=4，若点M、N满足$\overrightarrow{BM}=3\overrightarrow{MC}$，$\overrightarrow{DN}=2\overrightarrow{NC}$，则$\overrightarrow{AM}•\overrightarrow{NM}$=（　　）

• A． 20
• B． 15
• C． 9
• D． 6

Answer 1

分析 根据图形得出$\overrightarrow{AM}$=$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{BC}$=$\overrightarrow{AB}$$+\frac{3}{4}$$\overrightarrow{AD}$，
$\overrightarrow{AN}$=$\overrightarrow{AD}$$+\frac{2}{3}$$\overrightarrow{DC}$=$\overrightarrow{AD}$$+\frac{2}{3}$$\overrightarrow{AB}$，$\overrightarrow{AM}•\overrightarrow{NM}$=$\overrightarrow{AM}$•（$\overrightarrow{AM}$$-\overrightarrow{AN}$）=$\overrightarrow{AM}$²-$\overrightarrow{AM}$$•\overrightarrow{AN}$，
结合向量结合向量的数量积求解即可．

解答 解：∵四边形ABCD为平行四边形，点M、N满足$\overrightarrow{BM}=3\overrightarrow{MC}$，$\overrightarrow{DN}=2\overrightarrow{NC}$，
∴根据图形可得：$\overrightarrow{AM}$=$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{BC}$=$\overrightarrow{AB}$$+\frac{3}{4}$$\overrightarrow{AD}$，
$\overrightarrow{AN}$=$\overrightarrow{AD}$$+\frac{2}{3}$$\overrightarrow{DC}$=$\overrightarrow{AD}$$+\frac{2}{3}$$\overrightarrow{AB}$，
∴$\overrightarrow{NM}$=$\overrightarrow{AM}$$-\overrightarrow{AN}$，
∵$\overrightarrow{AM}•\overrightarrow{NM}$=$\overrightarrow{AM}$•（$\overrightarrow{AM}$$-\overrightarrow{AN}$）=$\overrightarrow{AM}$²-$\overrightarrow{AM}$$•\overrightarrow{AN}$，
$\overrightarrow{AM}$²=$\overrightarrow{AB}$²$+\frac{3}{2}$$\overrightarrow{AB}$$•\overrightarrow{AD}$$+\frac{9}{16}$$\overrightarrow{AD}$²，
$\overrightarrow{AM}$$•\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AB}$²$+\frac{3}{4}$$\overrightarrow{AD}$²$+\frac{3}{2}$$\overrightarrow{AB}$$•\overrightarrow{AD}$，
|$\overrightarrow{AB}$|=6，|$\overrightarrow{AD}$|=4，
∴$\overrightarrow{AM}•\overrightarrow{NM}$=$\frac{1}{3}\overrightarrow{AB}$²$-\frac{3}{16}$$\overrightarrow{AD}$²=12-3=9
故选：C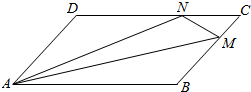

点评 本题考查了平面向量的运算，数量积的运用，考查了数形结合的思想，关键是向量的分解，表示．