题目内容
17.已知圆O:x2+y2=1,点M(x0,y0)是直线x-y+2=0上一点,若圆O上存在一点N,使得$∠NMO=\frac{π}{6}$,则x0的取值范围是[-2,0].分析 过M作⊙O切线交⊙C于R,则∠OMR≥∠OMN,由题意可得∠OMR≥$\frac{π}{6}$,|OM|≤2.再根据M(x0,2+x0),|OM|2=x02+y02=2x02 +4x0+4,求得x0的取值范围.
解答  解:过M作⊙O切线交⊙C于R,根据圆的切线性质,
解:过M作⊙O切线交⊙C于R,根据圆的切线性质,
有∠OMR≥∠OMN.
反过来,如果∠OMR≥$\frac{π}{6}$,则⊙O上存在一点N使得∠OMN=$\frac{π}{6}$.
∴若圆O上存在点N,使∠OMN=$\frac{π}{6}$,则∠OMR≥$\frac{π}{6}$.
∵|OR|=1,OR⊥MR,∴|OM|≤2.
又∵M(x0,2+x0),
|OM|2=x02+y02=x02+(2+x0)2=2x02 +4x0+4,
∴2x02+4x0+4≤4,解得,-2≤x0≤0.
∴x0的取值范围是[-2,0],
故答案为:[-2,0].
点评 本题主要考查了直线与圆相切时切线的性质,以及一元二次不等式的解法,综合考察了学生的转化能力,计算能力,属于中档题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
7.某校有6间不同的电脑室,每天晚上至少开放2间,求不同安排方案的种数,现有四位同学分别给出下列四个结果①$C_6^2$;②26-7;③$C_6^3+2C_6^4+C_6^5+C_6^6$,其中正确的结论是( )
| A. | ① | B. | ②与③ | C. | ①与② | D. | ①②③ |
8.随机询问某大学40名不同性别的大学生在购买食物时是否读营养说明,得到如下2×2列联表:
(1)根据以上列联表进行独立性检验,能否在犯错误的概率不超过0.01的前提下认为“性别与是否读营养说明之间有关系”?
(2)若采用分层抽样的方法从读营养说明的学生中随机抽取3人,则男生和女生抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求恰有一男一女的概率.
| 读营养说明 | 不读营养说明 | 合计 | |
| 男 | 16 | 4 | 20 |
| 女 | 8 | 12 | 20 |
| 合计 | 24 | 16 | 40 |
(2)若采用分层抽样的方法从读营养说明的学生中随机抽取3人,则男生和女生抽取的人数分别是多少?
(3)在(2)的条件下,从中随机抽取2人,求恰有一男一女的概率.
9.已知集合A={x|x2-2x-3≤0},B={x|-2≤x<2},则A∪B=( )
| A. | [-2,3] | B. | [-3,2] | C. | [-1,2] | D. | [-1,2) |
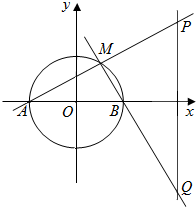 在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.
在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.