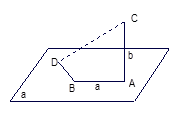
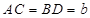题目内容
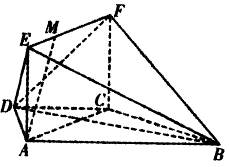
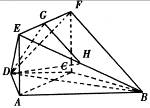
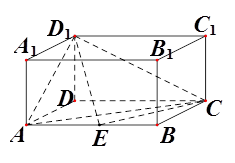
如图,在梯形 中
中 ‖
‖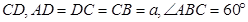 ,平面
,平面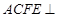 平面
平面 ,四边形
,四边形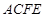 是矩形,
是矩形,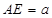 ,点
,点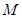 在线段
在线段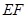 上.
上.
(Ⅰ)求证: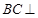 平面
平面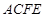 ;
;
(Ⅱ)当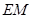 为何值时,
为何值时,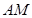 ‖平面
‖平面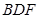 ?证明你的结论;
?证明你的结论;
(Ⅲ)求二面角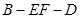 的大小.
的大小.
 中
中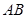 ‖
‖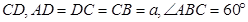 ,平面
,平面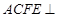 平面
平面 ,四边形
,四边形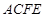 是矩形,
是矩形,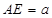 ,点
,点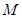 在线段
在线段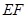 上.
上.(Ⅰ)求证:
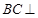 平面
平面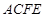 ;
;(Ⅱ)当
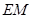 为何值时,
为何值时,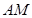 ‖平面
‖平面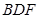 ?证明你的结论;
?证明你的结论;(Ⅲ)求二面角
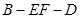 的大小.
的大小. 
(Ⅰ)在梯形ABCD中,∵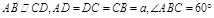 ,
,
∴四边形ABCD是等腰梯形,
且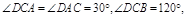
∴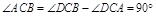 ,∴
,∴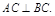
又∵平面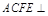 平面ABCD,交线为AC,∴
平面ABCD,交线为AC,∴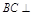 平面ACFE.
平面ACFE.
(Ⅱ)当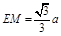 时,
时,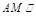 平面BDF. 在梯形ABCD中,设
平面BDF. 在梯形ABCD中,设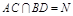 ,连结FN,则
,连结FN,则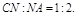
∵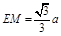 而
而 ,∴
,∴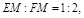 ∴MF
∴MF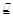 AN,
AN,
∴四边形ANFM是平行四边形. ∴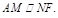
又∵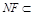 平面BDF,
平面BDF,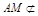 平面BDF. ∴
平面BDF. ∴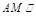 平面BDF.
平面BDF.
(Ⅲ)取EF中点G,EB中点H,连结DG、GH、DH,∵DE=DF,∴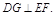 ∵
∵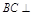 平面ACFE,∴
平面ACFE,∴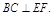 又∵
又∵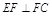 ,∴
,∴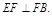 又∵
又∵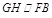 ,∴
,∴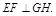
∴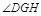 是二面角B—EF—D的平面角.
是二面角B—EF—D的平面角.
在△BDE中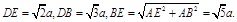 ∴
∴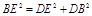 ∴
∴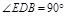 ,
,
∴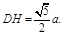 又
又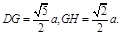 ∴在△DGH中,
∴在△DGH中,
由余弦定理得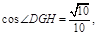 即二面角B—EF—D的大小为
即二面角B—EF—D的大小为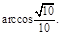
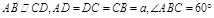 ,
,∴四边形ABCD是等腰梯形,
且
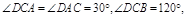
∴
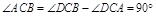 ,∴
,∴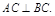

又∵平面
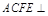 平面ABCD,交线为AC,∴
平面ABCD,交线为AC,∴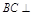 平面ACFE.
平面ACFE.(Ⅱ)当
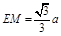 时,
时,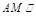 平面BDF. 在梯形ABCD中,设
平面BDF. 在梯形ABCD中,设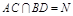 ,连结FN,则
,连结FN,则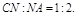
∵
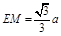 而
而 ,∴
,∴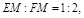 ∴MF
∴MF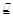 AN,
AN,∴四边形ANFM是平行四边形. ∴
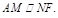
又∵
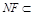 平面BDF,
平面BDF,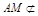 平面BDF. ∴
平面BDF. ∴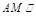 平面BDF.
平面BDF.(Ⅲ)取EF中点G,EB中点H,连结DG、GH、DH,∵DE=DF,∴
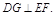 ∵
∵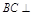 平面ACFE,∴
平面ACFE,∴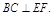 又∵
又∵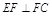 ,∴
,∴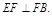 又∵
又∵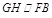 ,∴
,∴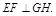
∴
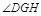 是二面角B—EF—D的平面角.
是二面角B—EF—D的平面角. 在△BDE中
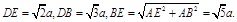 ∴
∴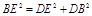 ∴
∴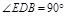 ,
,∴
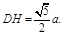 又
又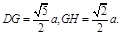 ∴在△DGH中,
∴在△DGH中,由余弦定理得
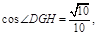 即二面角B—EF—D的大小为
即二面角B—EF—D的大小为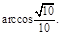
略

练习册系列答案
相关题目
 ,
, ,
,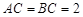 ,
, 在底面
在底面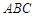 上的射影恰为
上的射影恰为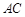 的中点
的中点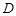 ,又知
,又知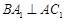 .
.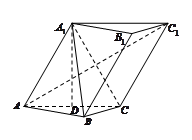
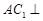 平面
平面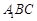 ;
; 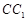 到平面
到平面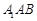 的距离;
的距离;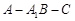 的大小。
的大小。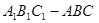 中,
中,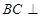 侧面
侧面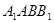 ,且
,且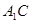 与底面成
与底面成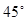 角,
角,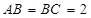 ,则该棱柱体积的 最小值为 .
,则该棱柱体积的 最小值为 . 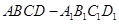 中,
中,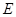 为
为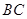 的中点,
的中点,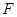 为
为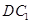 的中点.
的中点.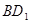 //平面
//平面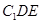 ;(2)求三棱锥
;(2)求三棱锥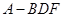 的体积;
的体积;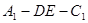 的余弦值。
的余弦值。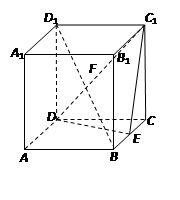
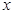 的圆柱.
的圆柱.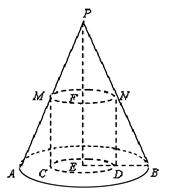
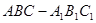 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,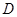 为
为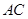 的中点.
的中点.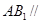 平面
平面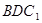 ;
;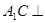 平面
平面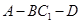 的正切值.
的正切值.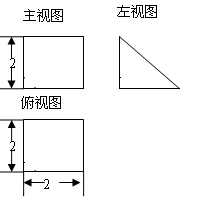
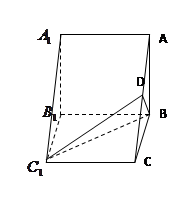
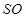 (
(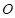 为底面中心)的侧面展开图,
为底面中心)的侧面展开图,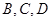 是其侧面展开图中弧
是其侧面展开图中弧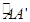 的四等分点,则在圆锥
的四等分点,则在圆锥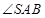 是直线
是直线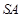 与
与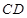 所成的角;
所成的角;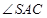 是直线
是直线 所成的角;
所成的角;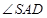 是二面角
是二面角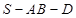 的平面角;
的平面角;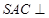 平面
平面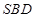
 角D1-EC-D的大小为
角D1-EC-D的大小为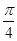 .
.
 内,线段
内,线段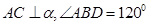 ,
, 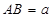 ,
,