题目内容
已知函数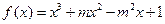 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.
(Ⅰ)求m的值;
(Ⅱ)若斜率为-5的直线是曲线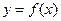 的切线,求此直线方程.
的切线,求此直线方程.
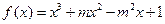 (m为常数,且m>0)有极大值9.
(m为常数,且m>0)有极大值9.(Ⅰ)求m的值;
(Ⅱ)若斜率为-5的直线是曲线
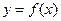 的切线,求此直线方程.
的切线,求此直线方程.解:(Ⅰ) f’(x)=3x2+2mx-m2=(x+m)(3x-m)=0,则x=-m或x=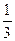 m,
m,
当x变化时,f’(x)与f(x)的变化情况如下表:
从而可知,当x=-m时,函数f(x)取得极大值9,即f(-m)=-m3+m3+m3+1=9,∴m=2.
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1,依题意知f’(x)=3x2+4x-4=-5,∴x=-1或x=-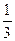 .
.
又f(-1)=6,f(-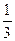 )=
)=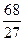 ,所以切线方程为y-6=-5(x+1),或y-
,所以切线方程为y-6=-5(x+1),或y-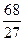 =-5(x+
=-5(x+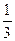 ),
),
即5x+y-1=0,或135x+27y-23=0.
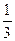 m,
m,当x变化时,f’(x)与f(x)的变化情况如下表:
| x | (-∞,-m) | -m | (-m,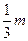 ) ) | 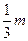 | (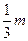 ,+∞) ,+∞) |
| f’(x) |  + + | 0 | - | 0 | + |
| f (x) | | 极大值 | | 极小值 | |
(Ⅱ)由(Ⅰ)知,f(x)=x3+2x2-4x+1,依题意知f’(x)=3x2+4x-4=-5,∴x=-1或x=-
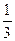 .
.又f(-1)=6,f(-
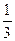 )=
)=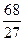 ,所以切线方程为y-6=-5(x+1),或y-
,所以切线方程为y-6=-5(x+1),或y-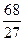 =-5(x+
=-5(x+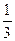 ),
),即5x+y-1=0,或135x+27y-23=0.
略

练习册系列答案
相关题目
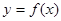 的导数
的导数 ,则
,则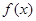 可以是
可以是 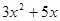
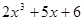
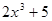
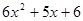
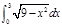 表示 ( )
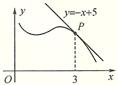
表示 ( )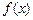 的图象在点P处的切线方程为y=-x+5,则
的图象在点P处的切线方程为y=-x+5,则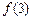 -
-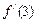 = .
= .
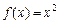 ,
,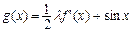 在[-1,1]上是减函数
在[-1,1]上是减函数 .
.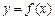 在点(1,
在点(1,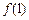 )处的切线方程;
)处的切线方程;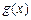 ≤
≤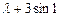 在x∈[-1,1]上恒成立,求
在x∈[-1,1]上恒成立,求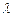 的取值范围;
的取值范围;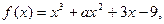 已知
已知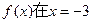 时取得极值,则
时取得极值,则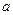 =" ( " )
=" ( " )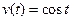 (
(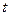 的单位为:秒,
的单位为:秒,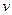 的单位为:米/秒)的速度作变速直线运动,该物体从时刻t=0秒至时刻 t=
的单位为:米/秒)的速度作变速直线运动,该物体从时刻t=0秒至时刻 t=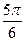 秒间运动的路程
秒间运动的路程 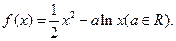
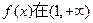 为增函数,求
为增函数,求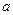 的取值范围
的取值范围 ;
;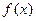 的零点个数,并说明理由。
的零点个数,并说明理由。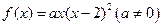 有极大值
有极大值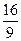 ,则
,则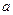 等于
等于

 (
(
