题目内容
11.将长为a的铁丝折成矩形,其中一条边长为x时,矩形的面积为y,则有( )| A. | y=-x2+ax,x∈(0,$\frac{a}{2}$) | B. | y=-x2+$\frac{a}{2}$x,x∈(0,a) | ||
| C. | y=-x2+$\frac{a}{2}$x,x∈(0,$\frac{a}{2}$) | D. | y=-2x2+ax,x∈(0,$\frac{a}{2}$) |
分析 由题意可得矩形的令一条边为$\frac{a-2x}{2}$,可得0<x<$\frac{a}{2}$,由矩形的面积公式可得.
解答 解:由题意可得矩形的令一条边为$\frac{a-2x}{2}$,
由$\frac{a-2x}{2}$>0可得x<$\frac{a}{2}$,结合x为边长可得0<x<$\frac{a}{2}$,
∴矩形的面积为y=x•$\frac{a-2x}{2}$=-x2+$\frac{a}{2}$x,0<x<$\frac{a}{2}$,
故选:C.
点评 本题考查函数解析式的求解,涉及矩形的面积公式,属基础题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
2.与函数y=$\frac{1}{\sqrt{x-1}}$有相同值域的函数是( )
| A. | y=$\frac{1}{x-1}$ | B. | y=ln(x-1) | C. | y=ex-1 | D. | y=|tanx| |
16.设方程2x=|log2(-x)|的两个根分别为x1,x2,则( )
| A. | x1x2<0 | B. | 0<x1x2<1 | C. | x1x2=1 | D. | x1x2>1 |
1.已知数列{an}的前n项和为Sn,若Sn=3n+2n+1,则an=( )
| A. | an=$\left\{\begin{array}{l}{6,n=1}\\{2×{3}^{n-1},n≥2}\end{array}\right.$ | B. | an=2×3n-1 | ||
| C. | an=2×3n-1+2 | D. | an=$\left\{\begin{array}{l}{6,n=1}\\{2×{3}^{n-1}+2,n≥2}\end{array}\right.$ |
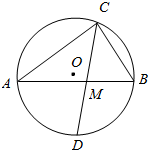 如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.
如图,已知AB是⊙O的直径,C为圆上一点,连接CB、AC,点D是半圆弧AB的中点,若圆的半径为4,DC交AB于M点,则DM•DC的范围是32.