题目内容
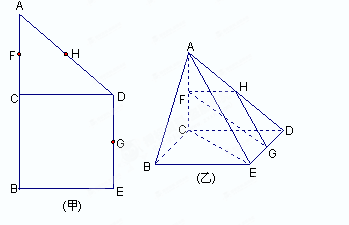
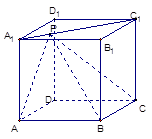
(本小题满分12分) 如图,在四棱锥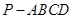 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱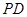 ⊥底面
⊥底面 ,
, ,
, 是
是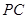 的中点,作
的中点,作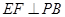 交
交 于点
于点
(1) 证明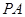 //平面
//平面 ;
;
(2) 证明 ⊥平面
⊥平面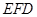 ;
;
(3) 求二面角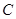 —
— —
—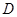 的大小。
的大小。
(1)证明:见解析;(2)证明:见解析;(3)二面角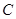 —
— —
—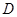 的大小为
的大小为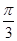
解析试题分析:(1)连结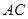 ,
,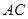 交
交 于O,连结
于O,连结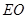
∵底面 是正方形,∴点O是
是正方形,∴点O是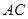 的中点
的中点
在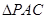 中,
中,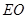 是中位线,∴
是中位线,∴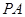 //
// 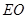 , 得到证明。
, 得到证明。
(2)∵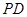 ⊥底面
⊥底面 且
且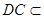 底面
底面 ,
,
∴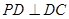 ∵
∵ ,可知
,可知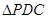 是等腰直角三角形,而
是等腰直角三角形,而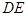 是斜边
是斜边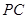 的中线,
的中线,
∴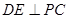 推理得到
推理得到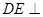 平面
平面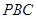
又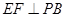 且
且 ,所以
,所以 ⊥平面
⊥平面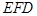 (3)由(2)知,
(3)由(2)知, ,
,
故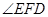 是二面角
是二面角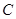 —
— —
—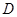 的平面角
的平面角
解:(1)证明:连结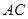 ,
,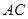 交
交 于O,连结
于O,连结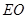
∵底面 是正方形,∴点O是
是正方形,∴点O是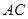 的中点
的中点
在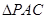 中,
中,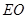 是中位线,∴
是中位线,∴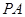 //
// 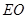 …(1分)
…(1分)
而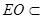 平面EDB且
平面EDB且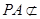 平面
平面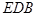 ,
,
所以,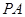 // 平面
// 平面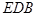 …(3分)
…(3分)
(2)证明:∵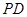 ⊥底面
⊥底面 且
且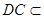 底面
底面 ,
,
∴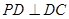
∵ ,可知
,可知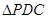 是等腰直角三角形,而
是等腰直角三角形,而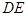 是斜边
是斜边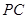 的中线,
的中线,
∴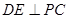 ① …(4分)
① …(4分)
同样由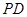 ⊥底面
⊥底面 ,得
,得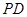 ⊥
⊥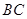
∵底面 是正方形,有DC⊥
是正方形,有DC⊥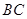 ,∴
,∴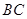 ⊥平面
⊥平面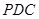 …(5分)
…(5分)
而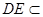 平面
平面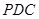 ,∴
,∴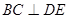 ②
②
由①和②推得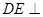 平面
平面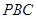
而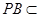

练习册系列答案
相关题目
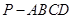 中,底面
中,底面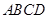 是矩形,
是矩形,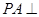 平面
平面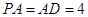 ,
,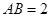 .
.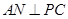 于点
于点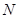 ,
, 是
是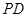 中点.
中点.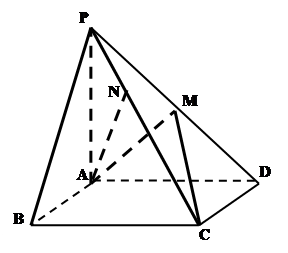
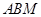 ⊥平面
⊥平面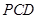 ;
; 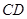 与平面
与平面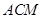 所成的角的正弦值;
所成的角的正弦值;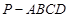 中,底面
中,底面 为矩形,
为矩形,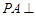 平面
平面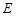 在线段
在线段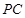 上,
上,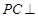 平面
平面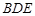 .
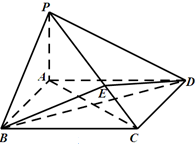
.
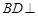 平面
平面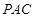 ;
;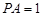 ,
,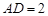 ,求二面角
,求二面角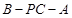 的正切值.
的正切值.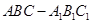 中,
中,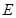 、
、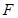 分别是
分别是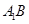 、
、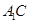 的中点,点
的中点,点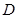 在
在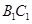 上,
上,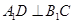 。
。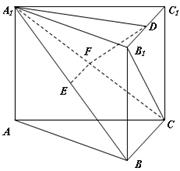
 平面
平面

 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值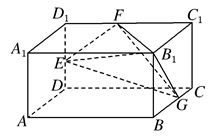
 平面
平面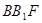 ;
;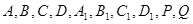 ;(2分)
;(2分)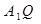 、
、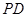 所成角为
所成角为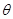 ,求
,求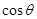 .(6分)
.(6分)

 BE,AB
BE,AB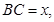
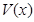 表示三棱锥B-ACE 的体积,求
表示三棱锥B-ACE 的体积,求