题目内容
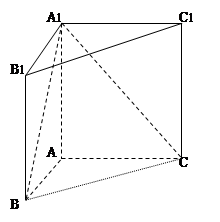
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.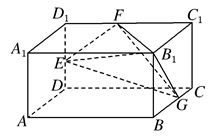
(1)求证:平面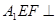 平面
平面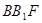 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
(1)见解析;
(2) H在A1D1上,且HD1=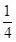 A1D1时,EH∥平面FGB1.
A1D1时,EH∥平面FGB1.
(3) V四面体EFGB1=VE—FGB1=VH—FGB1= ×1×
×1×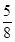 =
=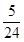 .
.
解析试题分析:(1)根据面面垂直的判定定理来得到证明。
(2)取A1D1的中点P,D1P的中点H,连接DP、EH,通过EH∥平面FGB1,说明EH∥B1G,得到HD1= 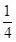 A1D1.
A1D1.
(3)以D为原点,直线DA、DC、DD1为x、y、z轴建立空间直角坐标系,利用法向量,求出E到平面FGB1的距离d,底面S△FGB1,然后求四面体EFGB1的体积.
解:(1)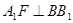
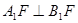

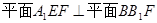
(2)取A1D1的中点P,D1P的中点H,连结DP、EH,则DP∥B1G,EH∥DP,
∴EH∥B1G,又B1G?平面FGB1,∴EH∥平面FGB1.
即H在A1D1上,且HD1=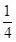 A1D1时,EH∥平面FGB1.
A1D1时,EH∥平面FGB1.
(3)∵EH∥平面FGB1,∴VE—FGB1=VH—FGB1,
而VH—FGB1=VG—HFB1= ×1×S△HFB1,
×1×S△HFB1,
S△HFB1=S梯形B1C1D1H-S△B1C1F-S△D1HF=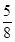 ,
,
∴V四面体EFGB1=VE—FGB1=VH—FGB1= ×1×
×1×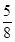 =
=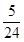 .
.
考点:本题主要考查了考查直线与平面的位置关系,探究点的位置,几何体的体积的求法,考查空间想象能力,计算能力.中档试题。
点评:解决该试题的关键是熟练的利用面面垂直的判定定理得到证明,同时能家里空间直角坐标系来表示平面的法向量,进而求解体积。

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 中,
中,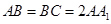
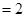 ,
, ,
, 是
是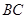 的中点.
的中点.
 平行平面
平行平面 ;
; 的余弦值;
的余弦值;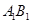 上是否存在点
上是否存在点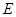 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定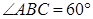 ,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.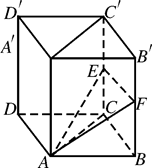
 中,四边形
中,四边形 为正方形,
为正方形, ,且
,且 ,
, 为
为 中点.
中点. //平面
//平面 ;
; 平面
平面 ;
; 的正弦值.
的正弦值.
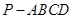 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱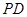 ⊥底面
⊥底面 ,
, 是
是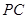 的中点,作
的中点,作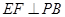 交
交 于点
于点
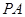 //平面
//平面 ;
;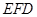 ;
;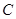 —
—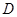 的大小。
的大小。
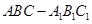 的侧面
的侧面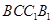 是菱形,
是菱形,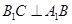 .
.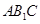
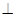 平面
平面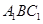 ;
;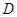 是
是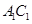 上的点,且
上的点,且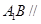 平面
平面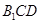 ,求
,求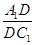 的值.
的值.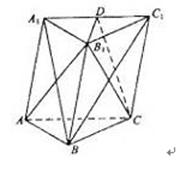
 ,
, 是垂足.
是垂足.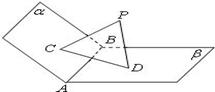
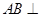 平面
平面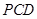 ;
; 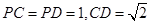 ,求证:
,求证:
 .
.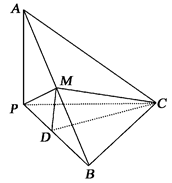
 中,
中,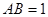 ,
,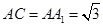 ,
, .
. ;
;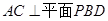
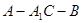 的正切值.
的正切值.