题目内容
(本小题满分12分)
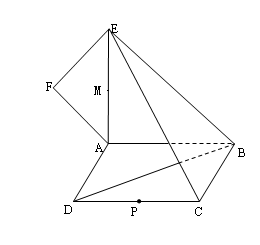
如图,在四棱锥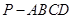 中,底面
中,底面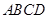 是矩形,
是矩形,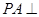 平面
平面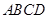 ,
,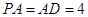 ,
,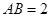 .
.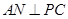 于点
于点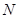 ,
, 是
是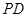 中点.
中点.
(1)用空间向量证明:AM⊥MC,平面 ⊥平面
⊥平面 ;
;
(2)求直线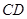 与平面
与平面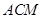 所成的角的正弦值;
所成的角的正弦值;
(3)求点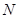 到平面
到平面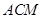 的距离.
的距离.
(1) ,
,


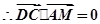
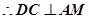
 平面
平面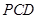 ,平面
,平面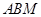 ⊥平面
⊥平面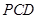
(2)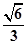 (3)
(3)
解析试题分析:以 为x轴,以
为x轴,以 为y轴,以
为y轴,以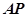 为z轴建立空间直角坐标系,则
为z轴建立空间直角坐标系,则 ,
,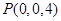 ,
, ,
, 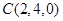 ,
,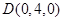 ,
,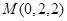 ;
;
(1) ,
,


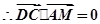
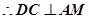
 平面
平面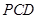 ,平面
,平面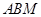 ⊥平面
⊥平面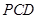
(2)设平面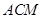 的一个法向量
的一个法向量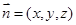 ,由
,由 可得:
可得: ,令
,令 ,则
,则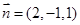 。设所求角为
。设所求角为 ,则
,则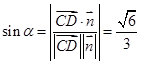
(3)由条件可得,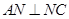 .在
.在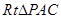 中,
中, ,所以
,所以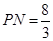 ,则
,则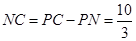 ,
, 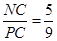 ,所以所求距离等于点
,所以所求距离等于点 到平面
到平面 距离的
距离的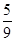 ,设点
,设点 到平面
到平面 距离为
距离为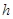 则
则 ,所以所求距离为
,所以所求距离为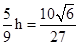 。
。
考点:向量法证明线面垂直求线面角求点面距
点评:采用空间向量的方法求解立体几何题目首先要建立合适的坐标系写出点的坐标,要求求解过程中对数据的计算要准确

练习册系列答案
相关题目
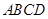 所在平面与平面四边形
所在平面与平面四边形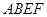 所在平面互相垂直,△
所在平面互相垂直,△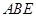 是等腰直角三角形,
是等腰直角三角形,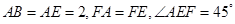
 的中点为
的中点为 ,线段
,线段 的中点为
的中点为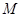 ,求证:
,求证: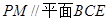 ;
;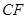 与平面
与平面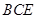 所成角的正切值.
所成角的正切值. ,VA =" 6."
,VA =" 6." 
 ,
, ,
, 是
是 的中点,
的中点, 是
是 中点.
中点.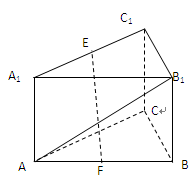
 ∥面
∥面 ;
; 所成角的正切值;
所成角的正切值;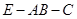 的平面角为
的平面角为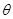 ,求
,求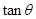 的值.
的值. 中,
中, 的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且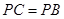 .
.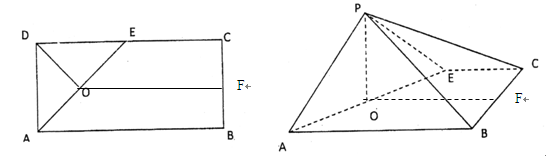
 中,
中,
 ,
, ,
, 是
是 的中点.
的中点.
 平行平面
平行平面 ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定 ,已知在四棱锥
,已知在四棱锥 中,底面
中,底面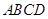 是矩形,
是矩形,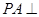 平面
平面 ,
, ,
,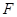 是
是 的中点,
的中点,  是线段
是线段 上的点.
上的点.
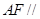 平面
平面 ;
; 的大小为
的大小为 ,试确定
,试确定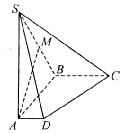
 ,求sin
,求sin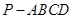 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱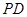 ⊥底面
⊥底面 ,
, 是
是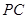 的中点,作
的中点,作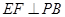 交
交 于点
于点
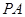 //平面
//平面 ;
;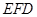 ;
;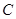 —
— 的大小。
的大小。