题目内容
(本小题满分14分)
如图,已知几何体的三视图(单位:cm).
(1)在这个几何体的直观图相应的位置标出字母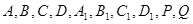 ;(2分)
;(2分)
(2)求这个几何体的表面积及体积;(6分)
(3)设异面直线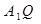 、
、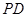 所成角为
所成角为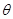 ,求
,求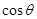 .(6分)
.(6分)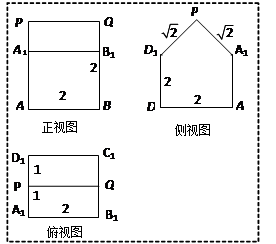

解(1)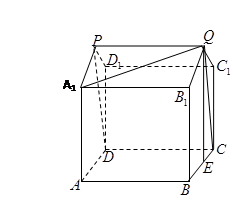
(2)几何体的全面积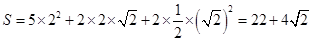
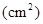 ;
;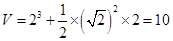
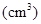 ;
;
(3异面直线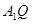 、
、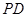 所成角的余弦值为
所成角的余弦值为 .
.
解析试题分析:(1)根据三视图的画出,进行复原画出几何体的图形即可.
(2)几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体,求出底面面积,然后求出体积即可.
(3)通过建立空间直角坐标系求解也可以,也能通过平移法得到异面直线的所成的角的大小,进而解得。
解(1)几何体的直观图相应的位置标出字母如图所示.…………2分 
(2)这个几何体可看成是由正方体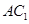 及直三棱柱
及直三棱柱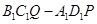 的组合体.
的组合体.
由 ,
,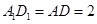 ,可得
,可得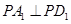 .
.
故所求几何体的全面积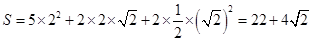
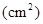 …5分
…5分
所求几何体的体积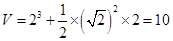
 ……8分
……8分
(3)由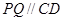 ,且
,且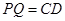 ,可知
,可知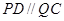 ,
,
故 为异面直线
为异面直线 、
、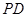 所成的角(或其补角).……10分
所成的角(或其补角).……10分
由题设知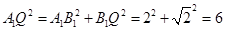 ,
,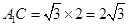 ,
,
取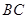 中点
中点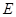 ,则
,则 ,且
,且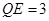 ,
, .……12分
.……12分
由余弦定理,得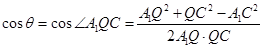
 .……13分
.……13分
所以异面直线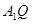 、
、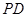 所成角的余弦值为
所成角的余弦值为 .………………14分
.………………14分
考点:本试题主要考查了三视图复原几何体,画出中逐步按照三视图的作法复原,考查空间想象能力,逻辑推理能力,计算能力,转化思想,是中档题.
点评:解决该试题的关键是能准确的由三视图得到原几何体,并能结合棱柱的体积和表面积公式准确运算,考查了一定的计算能力。

练习册系列答案
相关题目
(20) (本题满分14分) 已知正四棱锥P-ABCD中,底面是边长为2 的正方形,高为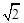 .M为线段PC的中点.
.M为线段PC的中点.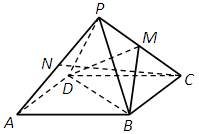
(Ⅰ) 求证:PA∥平面MDB;
(Ⅱ) N为AP的中点,求CN与平面MBD所成角的正切值.
 ,已知在四棱锥
,已知在四棱锥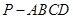 中,底面
中,底面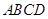 是矩形,
是矩形,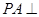 平面
平面 ,
, ,
,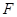 是
是 的中点,
的中点,  是线段
是线段 上的点.
上的点.
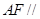 平面
平面 ;
; 的大小为
的大小为 ,试确定
,试确定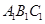 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为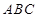 已知
已知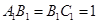 ,
,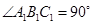 ,
,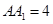 ,
,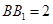 ,
,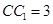

 是
是 的中点,证明:
的中点,证明: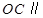 平面
平面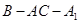 的大小;
的大小;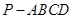 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱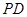 ⊥底面
⊥底面 ,
, 是
是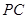 的中点,作
的中点,作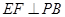 交
交 于点
于点
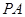 //平面
//平面 ;
;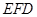 ;
;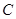 —
—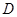 的大小。
的大小。
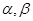 ,
,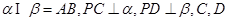 是垂足.
是垂足.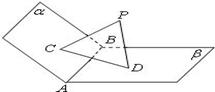
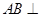 平面
平面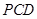 ;
; 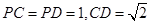 ,求证:
,求证: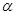
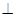
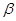 .
.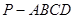 中,
中,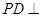 平面
平面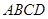 ,
,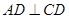 ,
,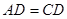 ,
,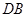 平分
平分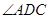 ,
,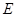 为
为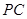 的中点.
的中点.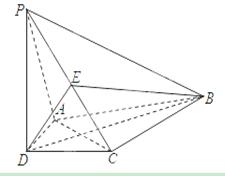
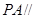 平面
平面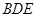 ;
;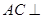 平面
平面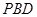 .
.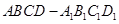 中,
中,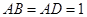 ,
,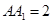 ,
,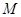 是棱
是棱 上一点,
上一点,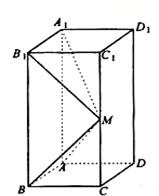
 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, .
.
 平面
平面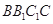 ;
; ,使得
,使得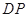 与平面
与平面 平行?证明你的结论.
平行?证明你的结论.