题目内容
(本小题11分)如图,三棱锥C—ABD,CB = CD,AB = AD,∠BAD = 90°。E、F分别是BC、AC的中点。
(1)求证:AC⊥BD;
(2)若CA = CB,求证:平面BCD⊥平面ABD
(3)在 上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出
上找一点M,在AD上找点N,使平面MED//平面BFN,说明理由;并求出 的值
的值
(1)见解析;(2)见解析;(3)2.
解析试题分析:(1)取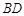 中点
中点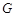 ,连接
,连接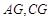
 中CB = CD,
中CB = CD,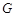 是
是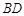 的中点,所以
的中点,所以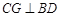
同理 中,
中,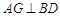 ,所以
,所以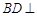 平面
平面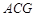 ,所以
,所以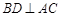 ………3分
………3分
(2)当CA = CB时,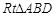 中,
中,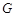 是
是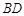 的中点,所以
的中点,所以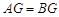
又 ,所以
,所以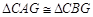 ,所以
,所以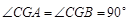 ,…………5分
,…………5分
即 ,又
,又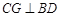 ,所以
,所以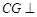 平面
平面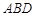
而 平面BCD,
平面BCD,
所以,平面BCD⊥平面ABD………………………………7分
(3)取CF中点M,连接MD,ED,在AD上取点N,使得 ……………9分
……………9分
因为M是CF中点,E是BC中点,所以ME//BF,又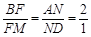
所以MD/NF,所以平面MED//平面BFN …………………11分
考点:线面垂直的性质定理;面面垂直的判定定理;线面平行的判判定定理。
点评:本题主要考查了“线与平面垂直”与“线与线垂直”的相互转化,线与平面的平行的判定及“线线平行”与“线面平行’的转化,考查了空间想象能力、推理论证的能力及对定理的熟练掌握。

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 中,
中, 的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
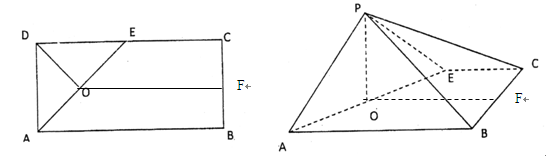
的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且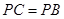 .
.
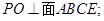
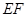 ⊥平面
⊥平面 ,
,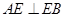 ,
,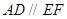 ,
,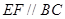 ,
,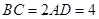 ,
,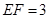 ,
,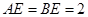 ,
,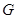 是
是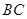 的中点.
的中点.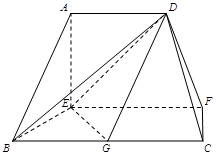
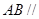 平面
平面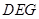 ;
;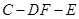 的余弦值.
的余弦值.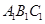 为底面)被一平面所截得到的几何体,截面为
为底面)被一平面所截得到的几何体,截面为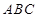 已知
已知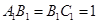 ,
,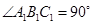 ,
,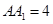 ,
,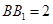 ,
,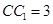

 是
是 的中点,证明:
的中点,证明: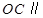 平面
平面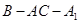 的大小;
的大小;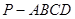 中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
中,平面PAD⊥平面 ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点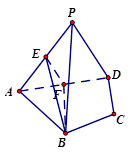
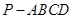 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱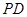 ⊥底面
⊥底面 ,
, 是
是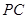 的中点,作
的中点,作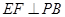 交
交 于点
于点
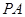 //平面
//平面 ;
;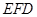 ;
;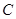 —
—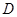 的大小。
的大小。
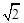 .M为线段PC的中点.
.M为线段PC的中点.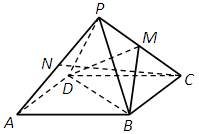
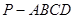 中,
中,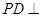 平面
平面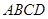 ,
,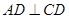 ,
,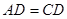 ,
,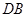 平分
平分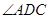 ,
, 为
为 的中点.
的中点.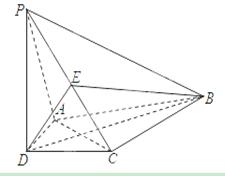
 平面
平面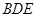 ;
;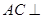 平面
平面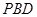 .
.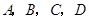 为空间四点.在
为空间四点.在 中,
中, .等边三角形
.等边三角形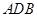 以
以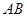 为轴运动.
为轴运动.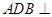 平面
平面 时,求
时,求 ;
;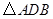 转动时,证明总有
转动时,证明总有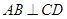 ?
?